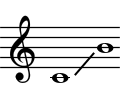Октавная система

Октавная система — способ группировки и обозначения музыкальных звуков на основе их октавного сходства.

Музыкальные звуки, частота которых отличается в два раза, воспринимаются на слух как очень похожие, как повторение одного звука на разной высоте. Это явление называется октавным сходством звуков. На основе этого весь диапазон частот используемых в музыке звуков делится на участки, называемые октавами, при этом частота звуков в каждой последующей октаве будет в два раза выше чем в предыдущей, а схожие звуки получают одинаковые названия ступеней.

Расположение частотных границ октав условно и выбрано таким образом, чтобы каждая октава начиналась с первой ступени («До») равномерно темперированного двенадцатизвукового строя и при этом частота 6-й ступени («Ля») одной из октав (называемой «первой») составляла бы 440 Гц.

Обозначения октав

Диапазон применимых в музыке звуков разбит на 9 октав, каждая из которых имеет своё название. Кроме того существуют разные способы обозначения принадлежности звука той или иной октаве, из которых наиболее распространены два — нотация Гельмгольца и научная нотация.

Наименования октав

Октава, лежащая посередине диапазона используемых в музыке звуков, называется «Первая октава», следующая вверх — «Вторая», затем «Третья», «Четвёртая» и «Пятая». Октавы ниже 1-й имеют собственные названия: «Малая октава» — это октава ниже 1-й, «Большая» — ниже малой, «Контроктава» — ниже большой и наконец «Субконтроктава» — ниже контроктавы — самая низкая из слышимых октав. Октавы ниже субконтроктавы и выше 5-й октавы выходят за диапазон применяемых в музыке звуков и потому не имеют собственных названий и обозначений звуков.

Нотация Гельмгольца

Была предложена немецким математиком Германом Гельмгольцем в своей работе Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik (1863)^[1]. Эта нотация основана на комбинации способа записи названия ступени — с большой либо маленькой буквы, числе штрихов рядом с названием ступени — от одного до пяти (вместо штрихов также используются арабские цифры) и места постановки штрихов — снизу либо сверху. Нотация Гельмгольца может быть применена как со слоговой системой наименования ступеней, так и с буквенной.

Научная нотация

Второй способ обозначения октав называется «научная система обозначения высоты звука». Впервые была предложена в 1939 году^[2] Американским Акустическим Обществом. В научной нотации номер октавы записывается сразу после обозначения ступени, при этом октавы нумеруются начиная с самой низкой слышимой (субконтроктавы), которой присваивается номер 0. Эта нотация применяется только с буквенной системой наименования ступеней.

Список октав^[3]

Субконтроктава

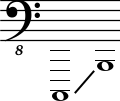
Включает звуки с частотами от 16,352 Гц (включительно) до 32,703 Гц. Самая низкая из слышимых октав, как правило нижние ступени этой октавы в музыке не используются. В нотации Гельмгольца наименования ступеней записываются с большой буквы и справа снизу ставится цифра 2 (или два штриха). В научной нотации имеет номер 0.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	16,352	До2	C2	C0
2	18,354	Ре2	D2	D0
3	20,602	Ми2	E2	E0
4	21,827	Фа2	F2	F0
5	24,500	Соль2	G2	G0
6	27,500	Ля2	A2	A0
7	30,868	Си2	H2*	H0

• В англоязычных странах используется модифицированная система Гельмгольца, вместо символа H для ноты «си» используется символ B, который в немецкой системе означает «си-бемоль».

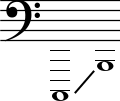
Контроктава

Включает звуки с частотами от 32.703 Гц (включительно) до 65.406 Гц. В нотации Гельмгольца наименования ступеней записываются с большой буквы и справа снизу ставится цифра 1 (или один штрих). В научной нотации имеет номер 1.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	32.703	До1	C1	C1
2	36.708	Ре1	D1	D1
3	41.203	Ми1	E1	E1
4	43.654	Фа1	F1	F1
5	48.999	Соль1	G1	G1
6	55.000	Ля1	A1	A1
7	61.735	Си1	H1	H1

Большая октава

Включает звуки с частотами от 65.406 Гц (включительно) до 130.81 Гц. В нотации Гельмгольца наименования ступеней записываются с большой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 2.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	65.406	До	C	C2
2	73.416	Ре	D	D2
3	82.406	Ми	E	E2
4	87.307	Фа	F	F2
5	97.999	Соль	G	G2
6	110.00	Ля	A	A2
7	123.47	Си	H	H2

Малая октава

Включает звуки с частотами от 130.81 Гц (включительно) до 261.63 Гц. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 3.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	130.81	до	c	C3
2	146.83	ре	d	D3
3	164.81	ми	e	E3
4	174.61	фа	f	F3
5	196.00	соль	g	G3
6	220.00	ля	a	A3
7	246.94	си	h	H3

Первая октава

Включает звуки с частотами от 261.63 Гц (включительно) до 523.25 Гц. Средняя октава звукоряда музыкальной системы. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 1 (или один штрих). В научной нотации имеет номер 4.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	261.63	до1	c1	C4
2	293.67	ре1	d1	D4
3	329.63	ми1	e1	E4
4	349.23	фа1	f1	F4
5	392.00	соль1	g1	G4
6	440.00	ля1	a1	A4
7	493.88	си1	h1	H4

Вторая октава

Включает звуки с частотами от 523.25 Гц (включительно) до 1046.5 Гц. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 2 (или два штриха). В научной нотации имеет номер 5.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	523.25	до2	c2	C5
2	587.33	ре2	d2	D5
3	659.26	ми2	e2	E5
4	698.46	фа2	f2	F5
5	783.99	соль2	g2	G5
6	880.00	ля2	a2	A5
7	987.77	си2	h2	H5

Третья октава

Включает звуки с частотами от 1046.5 Гц (включительно) до 2093.0 Гц. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 3 (или три штриха). В научной нотации имеет номер 6.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	1046.5	до3	c3	C6
2	1174.7	ре3	d3	D6
3	1318.5	ми3	e3	E6
4	1396.9	фа3	f3	F6
5	1568.0	соль3	g3	G6
6	1760.0	ля3	a3	A6
7	1975.5	си3	h3	H6

Четвёртая октава

Включает звуки с частотами от 2093.0 Гц (включительно) до 4186.0 Гц. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 4 (или четыре штриха). В научной нотации имеет номер 7.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	2093.0	до4	c4	C7
2	2349.3	ре4	d4	D7
3	2637.0	ми4	e4	E7
4	2793.8	фа4	f4	F7
5	3136.0	соль4	g4	G7
6	3520.0	ля4	a4	A7
7	3951.1	си4	h4	H7

Пятая октава

Включает звуки с частотами от 4186.0 Гц (включительно) до 8372.0 Гц. Самая высокая из используемых в музыке октав, верхние ступени (выше «До») применяются очень редко. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 5 (или пять штрихов). В научной нотации имеет номер 8.

Номер ступени	Частота, Гц	Слоговое обозначение по Гельмгольцу	Буквенное обозначение по Гельмгольцу	Научная нотация	Современная музыкальная нотация
1	4186.0	до5	c5	C8
2	4698.6	ре5	d5	D8
3	5274.0	ми5	e5	E8
4	5587.7	фа5	f5	F8
5	6271.9	соль5	g5	G8
6	7040.0	ля5	a5	A8
7	7902.1	си5	h5	H8

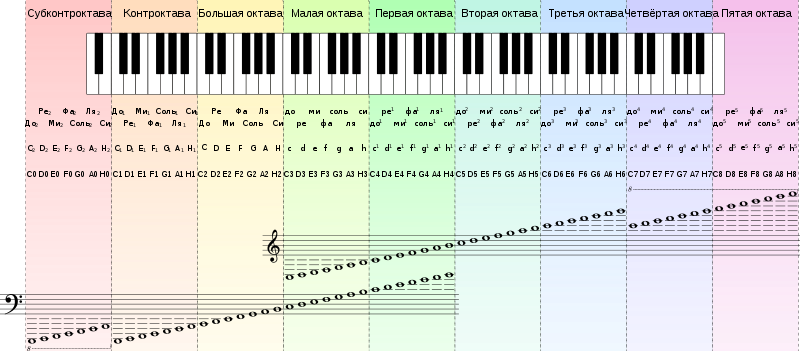
Схема

С помощью данной схемы или клавиатуры пианино возможно нахождение частоты звука. Для этого можно пользоваться следующей формулой:

$f = 27.5 \cdot 2^{\frac{n}{12}}$ (Гц),

где n — это порядковый номер ступени (на клавиатуре номер клавиши слева), начиная с «ля» субконтроктавы, отсчитывается с нуля.

Например, для нахождения частоты «ре» малой октавы n будет равно 29:

$27.5 \cdot 2^{\frac{29}{12}}=146.83$

Таблица соответствия нот частотам

Частоты в герцах (интервал от средней До в полутонах)
Октава → Нота ↓	Суб-контр	Контр	Большая	Малая	1	2	3	4	5	6
C	16.352 (−48)	32.703 (−36)	65.406 (−24)	130.81 (−12)	261.63 (0)	523.25 (+12)	1046.5 (+24)	2093.0 (+36)	4186.0 (+48)	8372.0 (+60)
C# / D♭	17.324 (−47)	34.648 (−35)	69.296 (−23)	138.59 (−11)	277.18 (+1)	554.37 (+13)	1108.7 (+25)	2217.5 (+37)	4434.9 (+49)	8869.8 (+61)
D	18.354 (−46)	36.708 (−34)	73.416 (−22)	146.83 (−10)	293.66 (+2)	587.33 (+14)	1174.7 (+26)	2349.3 (+38)	4698.6 (+50)	9397.3 (+62)
D# / E♭	19.445 (−45)	38.891 (−33)	77.782 (−21)	155.56 (−9)	311.13 (+3)	622.25 (+15)	1244.5 (+27)	2489.0 (+39)	4978.0 (+51)	9956.1 (+63)
E	20.602 (−44)	41.203 (−32)	82.407 (−20)	164.81 (−8)	329.63 (+4)	659.26 (+16)	1318.5 (+28)	2637.0 (+40)	5274.0 (+52)	10548 (+64)
F	21.827 (−43)	43.654 (−31)	87.307 (−19)	174.61 (−7)	349.23 (+5)	698.46 (+17)	1396.9 (+29)	2793.8 (+41)	5587.7 (+53)	11175 (+65)
F# / G♭	23.125 (−42)	46.249 (−30)	92.499 (−18)	185.00 (−6)	369.99 (+6)	739.99 (+18)	1480.0 (+30)	2960.0 (+42)	5919.9 (+54)	11840 (+66)
G	24.500 (−41)	48.999 (−29)	97.999 (−17)	196.00 (−5)	392.00 (+7)	783.99 (+19)	1568.0 (+31)	3136.0 (+43)	6271.9 (+55)	12544 (+67)
G# / A♭	25.957 (−40)	51.913 (−28)	103.83 (−16)	207.65 (−4)	415.30 (+8)	830.61 (+20)	1661.2 (+32)	3322.4 (+44)	6644.9 (+56)	13290 (+68)
A	27.500 (−39)	55.000 (−27)	110.00 (−15)	220.00 (−3)	440.00 (+9)	880.00 (+21)	1760.0 (+33)	3520.0 (+45)	7040.0 (+57)	14080 (+69)
A# / H♭	29.135 (−38)	58.270 (−26)	116.54 (−14)	233.08 (−2)	466.16 (+10)	932.33 (+22)	1864.7 (+34)	3729.3 (+46)	7458.6 (+58)	14917 (+70)
H	30.868 (−37)	61.735 (−25)	123.47 (−13)	246.94 (−1)	493.88 (+11)	987.77 (+23)	1975.5 (+35)	3951.1 (+47)	7902.1 (+59)	15804 (+71)
Примечание: Иногда нота Си обозначается как «B» вместо «H».

См. также

• Октава
• Нотные знаки
• Равномерно темперированный строй
• en:Helmholtz pitch notation
• en:Scientific pitch notation

Ссылки

• Английские наименования октав — Теория музыки на сайте, посвященном династии музыкантов Долмеч.

Литература

• Способин Игорь Владимирович Элементарная теория музыки. — М.: Музыка, 1968.
• Тюлин Юрий Николаевич Краткий теоретический курс гармонии. — М.: Музыка, 1978.

Примечания

1. ↑ Hermann von Helmholtz. (n.d.). A Dictionary of Scientists. Retrieved April 15, 2008, from Answers.com Web site: http://www.answers.com/topic/hermann-von-helmholtz
2. ↑ The Journal of the Acoustical Society of America — July 1939 — Volume 11, Issue 1, pp. 134—139
3. ↑ Значения частот рассчитаны исходя из стандартной частоты камертона ля¹ равной 440 Гц

Для улучшения этой статьи желательно?: Проставить интервики в рамках проекта Интервики.