Частица в периодическом потенциале

В квантовой механике, частица в одномерном периодическом потенциале — это идеализированная задача, которая может быть решена точно (при некоторых специального вида потенциалах), без упрощений. Предполагается, что потенциал бесконечен и периодичен, то есть обладает трансляционной симметрией, что, вообще говоря, не выполняется для реальных кристаллов, и всегда существует как минимум один дефект — поверхность (это приводит к другой задаче о поверхностных состояниях или таммовских уровнях).

Общий вид спектра

Периодическая задача

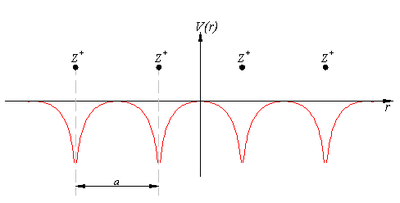
Рассмотрим одномерную решётку ионов, расстояние между которыми $\! a$. Потенциал при этом будет периодическим. Рассмотрим сначала идеализированный случай бесконечного кристалла. Уравнение Шрёдингера имеет вид:

$-\frac{\hbar^2}{2m}\frac{\partial^2 \psi (x)}{\partial x^2} + V_a(x) \psi (x) = E \psi (x)$

с периодическим потенциалом $V_a(x) = V_a(x+a).$ Спектр определяется как множество тех энергий, при которых уравнение имеет решения, ограниченные (не стремящиеся к нулю или бесконечности) на всей вещественной оси. Уравнение Шрёдингера имеет второй порядок, соответственно пространство решений является двумерным. Пусть $\psi_{1,2}$ — линейно независимые решения уравнения. Тогда при сдвиге на период, в силу периодичности задачи, они преобразуются через друг друга:

$\left( \begin{matrix} \psi_1(x+a) \\ \psi_2(x+a) \end{matrix} \right) = \mathrm{T} \left( \begin{matrix} \psi_1(x) \\ \psi_2(x) \end{matrix} \right)$

где $\mathrm{T}$ — некоторая матрица (матрица монодромии). Рассматривая вронскиан, несложно показать, что $\mathrm{T}$ унитарна и $\det \mathrm{T} = 1$. Отсюда следует, что в некотором базисе она имеет вид

$\mathrm{T} = \left( \begin{matrix} e^{\mathrm{i}kx} & 0 \\ 0 & e^{-\mathrm{i}kx} \end{matrix} \right)$

Отсюда следует теорема Блоха: соответствующие собственные функции имеют вид

$\psi_{1,2} (x) = e^{\mathrm{i}kx} \phi_{1,2}(x),$

где $\phi_{1,2}(x)$ — периодические функции. Заметим, что пока что $k\in\C$. Очевидно, что спектру соответствуют $k\in\R$, что равносильно (с учётом унитарности) условию на след матрицы монодромии

$\mathrm{Tr}\ \mathrm{T} = 2\cos(kx) \in [-2; 2]$

Несложно показать, что $\mathrm{Tr}( \mathrm{T})(E)$ есть гладкая функция. Отсюда следует зонная структура спектра: для частицы в периодическом потенциале допустимые уровни энергии — это некоторое, обычно бесконечное, множество отрезков на вещественной оси. Для потенциала общего вида спектр не имеет изолированных точек, при малом шевелении потенциала они либо исчезают, либо превращаются в зоны малой ширины. Заметим, что крайние отрезки спектра в принципе могут быть неограничены, при этом все уровни энергии, начиная с некоторого, являются допустимыми, а полное число зон конечно (см. конечнозонное интегрирование). В подобной постановке задача допускает полное и простое решение в тэта-функциях.

k называют квазиимпульсом, по аналогии с волновой функцией $e^{\mathrm{i}kx}$ для частицы с определённым импульсом k. Как видно, вся волновая функция определяется величиной k и любым участком функции длиной a.

Аналогично возникают энергетические зоны в решётках более высоких размерностей.

Влияние границ

В реальном кристалле число допустимых состояний, разумеется, конечно, хотя и очень велико. Приводящее к этому дополнительное ограничение на величину квазиимпульса возникает из граничных условий на волновую функцию на поверхности кристалла. При этом вместо непрерывных зон возникают области с плотно расположенными дискретными уровнями энергии (разрешённые зоны) и области, в которых состояний вообще нет (запрещённые зоны). Оценим расстояние между уровнями энергии в разрешённых зонах.

Вместо рассмотрения допустимых уровней энергии (для этого потребовалась бы дополнительная информация, вроде дисперсионного соотношения и точной структуры кристалла) рассмотрим допустимые значения квазиимпульса. При рассмотрении изолированного кристалла обычно рассматриваются периодические граничные условия на волновую функцию. Это предположение оправдано, так как точные граничные условия в реальном кристалле состоят в занулении волновой функции электронов на его границе. Для одномерного кристалла это означает чётность волновой функции (0 находится в центре кристалла). Если же влияние границ на волновую функцию мало́, то приближённо можно забыть про точное значение волновой функции на границе, сохранив лишь свойство симметрии — чётность.

Рассмотрим одномерный кристалл длины $L$. Граничное условие имеет вид

$\psi (0)=\psi (L)\,$

С учётом теоремы Блоха отсюда следует, что

$kL = 2\pi n,\; n\in\Z$

Таким образом, расстояние между соседними допустимыми значениями квазиимпульса равно

$\Delta k = \frac{2\pi n}{L}$

Аналогично в общем случае, для кубической решётки:

$\Delta k_{x,y,z} = \frac{2\pi n}{ L_{x,y,z} }$

Модель Кронига — Пенни

Для упрощения задачи потенциал приближают прямоугольным:

Используя теорему Блоха мы найдём волновую функцию во всём пространстве, но сначала надо найти решение для одного периода, и сделать его гладким на краях, то есть «сшить» значения соседних функций и их производных. Рассмотрим один период потенциала:
У нас есть две независимых области для которых мы найдём решения:

$0<x<a-b : {-\hbar^2 \over 2m} \psi_{xx} = E \psi$

$\Rightarrow \psi = A e^{i \alpha x} + A' e^{-i \alpha x} \quad \left( \alpha^2 = {2mE \over \hbar^2} \right)$

$-b<x<0 : {-\hbar^2 \over 2m} \psi_{xx} = (E+V_0)\psi$

$\Rightarrow \psi = B e^{i \beta x} + B' e^{-i \beta x} \quad \left( \beta^2 = {2m(E+V_0) \over \hbar^2} \right)$

Для нахождения u(x) в каждой области нужно проделать следующие преобразования:

$\psi(0<x<a-b) = A e^{i \alpha x} + A' e^{-i \alpha x} = e^{ikx} \cdot \left( A e^{i (\alpha-k) x} + A' e^{-i (\alpha+k) x} \right)$

$\Rightarrow u(0<x<a-b)=A e^{i (\alpha-k) x} + A' e^{-i (\alpha+k) x}$

Аналогично получим

$u( -b<x<0)=B e^{ i (\beta - k) x} + B' e^{ - i ( \beta + k ) x} \;$

Чтобы найти полное решение нам надо убедиться в гладкости искомой функции на границах:

$\psi(0^{-})=\psi(0^{+}) \quad \psi'(0^{-})=\psi'(0^{+})$

и периодичности u(x) и u'(x)

$u(-b)=u(a-b) \quad u'(-b)=u'(a-b).\,$

Эти условия дают следующую матрицу:

$\begin{pmatrix} 1 & 1 & -1 & -1 \\ \alpha & -\alpha & -\beta & \beta \\ e^{i(\alpha-k)(a-b)} & e^{-i(\alpha+k)(a-b)} & -e^{-i(\beta-k)b} & -e^{i(\beta+k)b} \\ (\alpha-k)e^{i(\alpha-k)(a-b)} & (\alpha+k)e^{-i(\alpha+k)(a-b)} & -(\beta-k)e^{-i(\beta-k)b} & (\beta+k)e^{i(\beta+k)b} \end{pmatrix} \begin{pmatrix} A \\ A' \\ B \\ B' \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}$

Для существования нетривиального решения необходимо зануление детерминанта этой матрицы. После некоторых преобразований получаем:

$\cos(k a) = \cos(\beta b) \cos[\alpha(a-b)]-{\alpha^2+\beta^2 \over 2\alpha \beta} \sin(\beta b) \sin[\alpha(a-b)]. \qquad ( * )$

Для дальнейшего упрощения мы выполним следующие упрощения, смысл которых заключается в переходе к дельта-образным потенциалам (дираковская гребёнка) :

$b \rightarrow 0 \ ; \ V_0 \rightarrow \infty \ ; \ V_0 b = \mathrm{constant}$

$\Rightarrow \beta b \rightarrow 0 \ ; \ \beta^2 b = \mathrm{constant} \ ; \ \alpha^2 b \rightarrow 0 \ ; \ \sin(\beta b) \rightarrow \beta b \ ; \ \cos(\beta b) \rightarrow 1$

Тогда конечный ответ будет:

$\cos(k a) = \cos(\alpha a)-P{\sin(\alpha a) \over \alpha a} \qquad \left( P={\beta^2 a b \over 2} \right)$

Программный код

Код для Maple

Следующий программный код написан на языке Maple (9.5). Представляет собой просто графическое решение $( * )$.

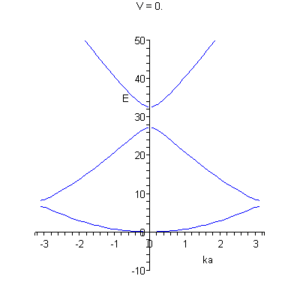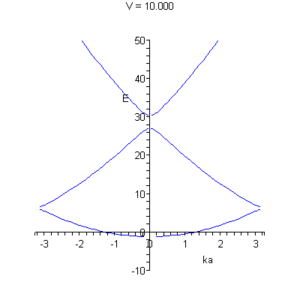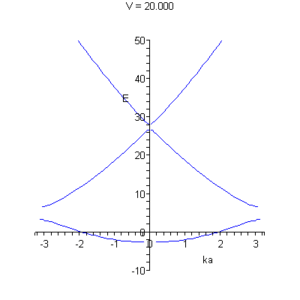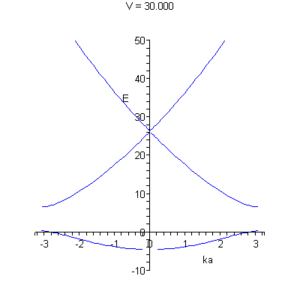
  restart;
  with(plots):
  with(stats[statplots]):
  eq:=cos(k*a)=cos(beta*b)*cos(alpha*(a-b)) - (alpha^2+beta^2)/(2*alpha*beta)*sin(beta*b)*sin(alpha*(a-b));
  alpha:=sqrt(8*Pi^2*m*(E)*e/h^2):
  beta:=sqrt(8*Pi^2*m*(E+V)*e/h^2):
  e:=1.6*1e-19:
  a:=0.54310*1e-9:
  m:=0.19*9.1*1e-31:
  b:=1/5*a:
  h:=6.6*1e-34:
  k(E,V):=arccos(rhs(evalf(eq)));

  #График
  p:=plot({subs(V=10,k(E,V)),subs(V=10,-k(E,V))},E=-5..50,labels=[ka, E],color=blue):
  xyexchange(p);

  #Анимация, зависимость от глубины ямы
  p:=animate( plot, [{k(E,V),-k(E,V)},E=-10..50, color=blue,labels=[ka, E]], V=0..30 ):
  xyexchange(p);

На рисунках представлены графические решения уравнения ( * ).

Линии отвечают разрешённым значениям энергии. Существуют области по энергии, где ни при каких значениях волнового вектора невозможно существование электрона. Линии отвечают разрешённым значениям энергии. Показано движение закона дисперсии в зависимости от глубины потенциальной ямы. На правом рисунке видно, как при некотором значении потенциальной энергии возможно образование одномерного бесщелевого полупроводника.

Код для Scilab

Линии по-прежнему отвечают разрешённым значениям энергии. Синим изображено решение для модели Кронига-Пенни, красным - гребёнки Дирака при тех же значениях V₀b

Код ниже является фактически переводом предшествующей программы на язык Scilab, за тем исключением, что иллюстрирует также и случай перехода к гребёнке Дирака.

clear all
 
global Pi e a m b h
 
Pi = 3.1415926;
 
step = 0.1;
 
e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;
 
function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(8*Pi^2*m*(E+V)*e/h^2);
endfunction
 
function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) / (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
endfunction
 
function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) / 2 .* sin(alpha*a) / (alpha * a));
endfunction
 
E = [0 : step: 50];
 
k = kronigpenney(10, E);
plot(k, E, 'b'); plot(-k, E, 'b');
 
k = dirac(10, E);
plot(k, E, 'r'); plot(-k, E, 'r');

Код для Matlab

Код ниже является переводом предшествующей программы на язык Matlab.

function KronigPenneyM
 
% clear all
% global Pi e a m b h
Pi = 3.1415926;
step = 0.1;
 
e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;
 
E = [0 : step: 50];
N = 3;
 
hold on; 
k = kronigpenney(N, E);
plot([real(k) NaN, -real(k)], [E NaN E], 'b');
 
k = dirac(N, E);
plot([real(k) NaN, -real(k)], [E NaN E], 'r');
 
function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(8*Pi^2*m*(E+V)*e/h^2);
end
 
function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) / (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
end
 
function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) / 2 .* sin(alpha*a) / (alpha * a));
end
end

Ссылки

• Задачи по квантовой механике. Часть 1. Галицкий, Карнаков, Коган.
• 1-D periodic potential applet
• Energy band formation

См. также

Квантовая яма

Оптическая решетка