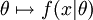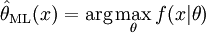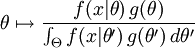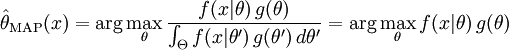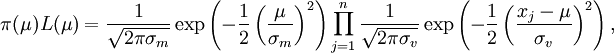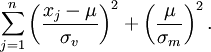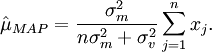- Максимальная апостериорная гипотеза
-
В статистике метод оценки Максимальной апостериорной гипотезы (MAP) тесно связан с методом максимального правдоподобия (ML), но использует дополнительную оптимизацию, которая совмещает априорное распределение величины, которую хочет оценить.
Введение
Предположим, что нам нужно оценить неконтролируемый параметр выборки θ на базе наблюдений x. Пусть f - выборочное распределение x, такое, что f(x | θ) - вероятность x в то время как параметр выборки θ. Тогда функция
известна как функция правдоподобия, а оценка
как оценка максимального правдоподобия θ.
Теперь, предположим, что априорное распределение g на θ существует. Это позволяет рассматривать θ как случайную величину как в Байесовой статистике. тогда апостериорное распределение θ:
где g плотность распределения Θ, Θ - область определения g. Это прямое приложение Теоремы Байеса.
Метод оценки максимального правдоподобия затем оценивает θ как апостериорное распределение этой случайной величины:
Знаменатель апостериорного распределения не зависит от θ и поэтому не играет роли в оптимизации. Заметим, что MAP оценка θ соответствует ML оценке когда априорная g постоянна (т.е., константа).
Пример
Предположим, что у нас есть последовательность
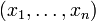 IID
IID 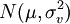 случайных величин и априорное распределение μ задано
случайных величин и априорное распределение μ задано 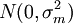 . Мы хотим найти MAP оценку μ.
. Мы хотим найти MAP оценку μ.Функция, которую нужно максимизировать задана
что эквивалентно минимизации μ в
Таким образом, мы видим, что MAP оценка для μ задана
Ссылки
- M. DeGroot, Optimal Statistical Decisions, McGraw-Hill, (1970).
- Harold W. Sorenson, (1980) "Parameter Estimation: Principles and Problems", Marcel Dekker.
- EM-алгоритм - один из способов вычисления MAP
- Метод максимального правдоподобия
Wikimedia Foundation. 2010.