- Сети Петри
-
Сети Петри — математический аппарат для моделирования динамических дискретных систем. Впервые описаны Карлом Петри в 1962 году.
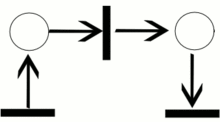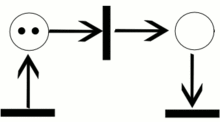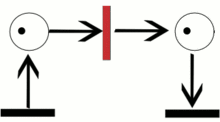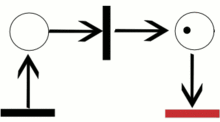
Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами. Вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.
Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, либо разновременно, при выполнении некоторых условий.
Содержание
История
Сети Петри разрабатывались для моделирования систем с параллельными взаимодействующими компонентами. Сети Петри впервые предложил Карл Адам Петри. В докторской диссертации "Связь автоматов" он сформулировал основные понятия теории связи асинхронных компонент вычислительной системы[1].
Виды сетей Петри
Некоторые виды сетей Петри:
- Временная сеть Петри — переходы обладают весом, определяющим продолжительность срабатывания (задержку).
- Стохастическая сеть Петри — задержки являются случайными величинами.
- Функциональная сеть Петри — задержки определяются как функции некоторых аргументов, например, количества меток в каких-либо позициях, состояния некоторых переходов.
- Цветная сеть Петри — метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях.
- Ингибиторная сеть Петри — возможны ингибиторные дуги, запрещающие срабатывания перехода, если во входной позиции, связанной с переходом ингибиторной дугой, находится метка.
- Иерархическая сеть — содержит не мгновенные переходы, в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого перехода характеризует выполнение полного жизненного цикла вложенной сети.
- WF-сети
Анализ сетей Петри
Основными свойствами сети Петри являются:
- ограниченность — число меток в любой позиции сети не может превысить некоторого значения K;
- безопасность — частный случай ограниченности, K=1;
- сохраняемость — постоянство загрузки ресурсов,
 постоянна. Где
постоянна. Где  — число маркеров в i-той позиции,
— число маркеров в i-той позиции,  — весовой коэффициент;
— весовой коэффициент; - достижимость — возможность перехода сети из одного заданного состояния (характеризуемого распределением меток) в другое;
- живость — возможность срабатывания любого перехода при функционировании моделируемого объекта.
В основе исследования перечисленных свойств лежит анализ достижимости.
См. также
Примечания
- ↑ Джеймс Питерсон Теория сетей Петри и моделирование систем:Пер. с англ.-М.:Мир, 1984.-264с., ил. (стр. 11 "1.3. Зарождение теории сетей Петри")
Ссылки
- Учебный курс МГТУ им. Баумана «Основы САПР. Моделирование». Сети Петри. Анализ сетей Петри
- Сети Петри на сайте Института автоматики и процессов управления.
- Исходные тексты примеров программ, реализующих сети Петри и строго иерархические сети.
 Категория:
Категория:- Сети Петри
Wikimedia Foundation. 2010.