- Четырёхполюсник
-
Четырёхпо́люсник — многополюсник, имеющий четыре точки подключения. Как правило, две точки являются входом, две другие — выходом.
Содержание
Общие сведения
При анализе электрических цепей очень часто бывает удобным выделить фрагмент цепи, имеющий две пары зажимов. Поскольку электрические (электронные) цепи очень часто связаны с передачей энергии или обработкой и преобразованием информации, одну пару зажимов обычно называют «входными», а вторую — «выходными». На входные зажимы подаётся исходный сигнал, с выходных снимается преобразованный.
Такими четырёхполюсниками являются, например, трансформаторы, усилители, фильтры, стабилизаторы напряжения, телефонные линии, линии электропередачи и т. д.
Однако математическая теория четырёхполюсников не предполагает никаких преопределённых потоков энергии/информации в цепях, поэтому названия «входные» и «выходные» являются данью традиции и с этой оговоркой будут использоваться далее.
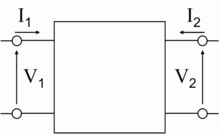
Состояния входных и выходных зажимов определяются четырьмя параметрами: напряжением и током во входной (U1, I1) и выходной (U2, I2) цепях. В этой системе параметров линейный четырёхполюсник описывается системой из двух линейных уравнений, причём два из четырёх параметров состояния являются исходными, а два остальные — определяемыми. Для нелинейных четырёхполюсников зависимость может носить более сложный характер. Например, выходные параметры через входные можно выразить системой
В дальнейшем будет использоваться запись системы уравнений в матричном виде, как наиболее удобная для восприятия.
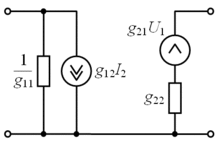
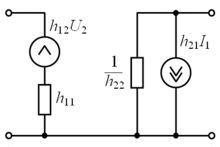
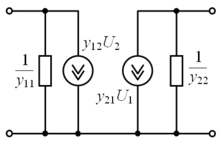
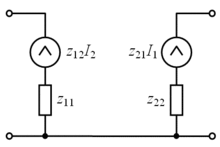
Поскольку четырёхполюсник имеет четыре параметра состояния, очевидно, что имеется шесть систем уравнений, выражающих различные пары параметров через два остальных. Коэффициенты этих шести систем уравнений получили традиционное наименование A-, B-, G-, H-, Y- и Z-параметров. Системы уравнений и эквивалентные схемы четырёхполюсников при использовании каждого типа параметров показаны в таблице.1
Системы параметров
Системы уравнений, эквивалентные схемы, измерение параметров
Тип Система уравнений Эквивалентная схема Измерение параметров 























Преобразование параметров
Принцип преобразованияВ качестве примера преобразуем h-параметры четырёхполюсника в y-параметры. Для этого нужно осуществить следующее преобразование системы уравнений:
Из первого уравнения исходной системы выразим I1:
Первое уравнение подставим во второе:
Преобразуем второе уравнение:
где

Получаем систему уравнений
Сравнивая её с целевой системой, получаем выражения для коэффициентов:
Определитель новой системы находим простой подстановкой:






































































































Преобразования схем
Rin, Rout — входное и выходное сопротивления; KI, KU — коэффициенты усиления по току и напряжению.

Схема 



















 Принцип вычисления параметров схемы
Принцип вычисления параметров схемыВ качестве примера найдем входное/выходное сопротивление и коэффициенты усиления по току и напряжению для четырёхполюсника, описанного h-параметрами.
- Входное сопротивление
Ненагруженный четырёхполюсник описывается системой
При подключении нагрузки
Преобразуем систему уравнений
Описание четырёхполюсника
Линейный четырёхполюсник, не содержащий независимых источников (напряжения и/или тока), описывается четырьмя параметрами (из которых только три являются независимыми). Как правило, используется одна из шести систем формальных параметров четырёхполюсника:
- система а-параметров
- система z-параметров
- система y-параметров
- система h-параметров
- система g-параметров
- система b-параметров
Конкретная система выбирается из соображений удобства. Выбор зависит от того, какой параметр (напряжение или ток) является входным и какой — выходным сигналом для данного четырёхполюсника.
В указанных системах формальных параметров не могут быть учтены произвольные внутренние источники (например, постоянного тока), допускаются только управляемые генераторы тока и управляемые генераторы напряжения, которые управляются входными сигналами четырёхполюсника. Поэтому в качестве четырёхполюсников рассматриваются, как правило, эквивалентные схемы по переменному току.
Существуют два типа вторичных параметров четырёхполюсников:
- Характеристические сопротивления Zc
- постоянные передачи Г.
Но как правило они используются для расчёта и исследования каскадного соединения одинаковых четырёхполюсников.
Также существуют
Симметричный четырёхполюсник — четырёхполюсник, у которого схема одинакова относительно его входных и выходных зажимов. Тогда для симметричного четырёхполюсника Z11 = Z22. Ещё: если при перемене местами источника и приемника энергии их токи не меняются, то такой четырёхполюсник называется симметричным.
Пассивный четырёхполюсник — это четырёхполюсник, который не содержит источников энергии, либо содержит скомпенсированные источники энергии.
Активный четырёхполюсник — это четырёхполюсник, который содержит нескомпенсированные источники энергии.
Обратимый четырёхполюсник — четырёхполюсник, у которого выполняется теорема обратимости, то есть передаточное сопротивление входных и выходных контуров не зависят от того, какая пара зажимов входная, а какая выходная: U1/I2=U2/I1
Категория:- Эквивалентные схемы
Wikimedia Foundation. 2010.















![~U_1(1+h_{22}R) = I_1[h_{11}(1+h_{22}R)-h_{12}h_{21}R ];](612e29be0acf98b10e4f9d0b832a65ab.png)


