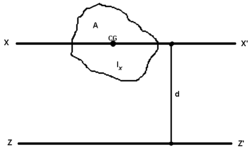
Теорема Гюйгенса-Штейнера

Иллюстрация теоремы для момента площади.

Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела $J$ относительно произвольной оси равен сумме момента инерции этого тела $J_C$ относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела $m$ на квадрат расстояния $d$ между осями:

$J=J_C+md^2\,\!$

где

$J_C$ — известный момент инерции относительно оси, проходящей через центр масс тела,

$J$ — искомый момент инерции относительно параллельной оси,

$m$ — масса тела,

$d$ — расстояние между указанными осями.

Вывод

Момент инерции, по определению:

$J=\sum_{i=1}^n m_i (\vec{r'}_i)^2\,\!$

Радиус-вектор $\vec{r'}_i\,\!$ можно расписать как разность двух векторов:

$\vec{r'}_i=\vec{r}_i-\vec{d}\,\!$,

где $\vec{d}$ — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

$J=\sum_{i=1}^n m_i (\vec{r}_i)^2 - 2 \sum_{i=1}^n m_i \vec{r}_i \vec{d} + \sum_{i=1}^n m_i (\vec{d})^2\,\!$

Вынося за сумму $\vec{d}$, получим:

$J=\sum_{i=1}^n m_i (\vec{r}_i)^2 - 2 \vec{d} \sum_{i=1}^n m_i \vec{r}_i + d^2 \sum_{i=1}^n m_i \,\!$

Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

$\sum_{i=1}^n m_i \vec{r}_i=0\,\!$

Тогда:

$J=\sum_{i=1}^n m_i (\vec{r}_i)^2 + d^2 \sum_{i=1}^n m_i \,\!$

Откуда и следует искомая формула:

$J=J_C + m d^2\,\!$,

где $J_C$ — известный момент инерции относительно оси, проходящей через центр масс тела.

Пример

Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью $C$) равен

$J_C=\frac{mL^2}{12}.$

Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен

$J=J_C+md^2\,\!$

где $d$ — расстояние между искомой осью и осью $C$. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле $d=L/2$:

$J=J_C+m\left(\frac{L}{2}\right)^2=\frac{mL^2}{12}+\frac{mL^2}{4}=\frac{mL^2}{3}.$

Пересчёт тензора инерции

Теорема Гюйнеса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор $\mathbf{J}_{ij}$ относительно произвольной точки из тензора $\mathbf{I}_{ij}$ относительно центра масс. Пусть $\mathbf{a}$ — смещение от центра масс, тогда

$\mathbf{J}_{ij}=\mathbf{I}_{ij}+m(a^2\delta_{ij}-a_ia_j),$

где

$\mathbf{a}=a_1\mathbf{\hat{x}}+a_2\mathbf{\hat{y}}+a_3\mathbf{\hat{z}}$ — вектор смещения от центра масс, а $\delta_{ij}$ — символ Кронекера.

Как видно, для диагональных элементов тензора (при $i=j$) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси.

См. также

• Момент инерции
• Список моментов инерции

Для улучшения этой статьи по физике желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Проставив сноски, внести более точные указания на источники.