Формула поворота Родрига

Формула поворота Родрига — формула, связывающая два вектора с общим началом, один из которых получен поворотом другого на известный угол вокруг оси, проходящей через их общее начало:

$\vec{R}_2 - \tan(\chi/2) [\vec{e} \times \vec{R}_2] = \vec{R}_1 + \tan(\chi/2) [\vec{e} \times \vec{R}_2]$

где $\vec{R}_1$ — исходный вектор, $\vec{R}_2$ — результирующий вектор, $\vec{e}$ — единичный вектор оси поворота, $\chi$ — угол поворота.

Так же формула записывается в виде:

$\vec{R}_2 = (\vec{e} \cdot \vec{R}_1)(1-\cos\chi) \vec{e} + (\vec{e} \times \vec{R}_1)\sin\chi + \vec{R}_1 \cdot \cos \chi$

Лежит в основе векторной теории конечных поворотов и сложения вращений.

Вывод

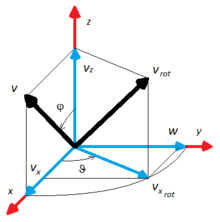
Без потери общности, направим ось $\vec{z}$ вдоль единичного вектора $\vec{e}$, а вектор $\vec{R}_1$ — лежащим в плоскости OXZ, тогда:

$\vec{R}_{1x} = \vec{R}_1 - \vec{R}_{1z}$

$\vec{R}_{1y} = 0$

$\vec{R}_{1z} = (\vec{e} \cdot \vec{R}_1) \vec{e}$

Откуда:

$\vec{R}_{1x} = \vec{R}_1 - (\vec{e} \cdot \vec{R}_1) \vec{e}$

Положим вектор $\vec{w}$, равный:

$\vec{w} = \vec{e}\times\vec{R}_1$

Заметим, что:

$|\vec{w}| = |\vec{e} \times \vec{R}_1| = |\vec{e}| \, |\vec{R}_1| \sin \phi \ = |\vec{R}_1| \sin \phi$

$|\vec{R}_{1x}| = |\vec{R}_1| \cos(\pi/2-\phi) = |\vec{R}_1| \sin \phi.$

Тогда вектор $\vec{u}_x$ можно выразить через векторы $\vec{w}$ и $\vec{R}_{1x}$ и угол $\chi$:

$\vec{R}_{2x} = \vec{R}_{1x}\cos\chi + \vec{w}\sin\chi = (\vec{R}_1 - (\vec{e} \cdot \vec{R}_1) \vec{e})\cos\chi + (\vec{e} \times \vec{R}_1)\sin\chi$

Результирующий вектор $\vec{R}_2$ выражается через векторы $\vec{R}_{2x}$ и $\vec{R}_{1z}$:

$\vec{R}_2 = \vec{R}_{2x} + \vec{R}_{1z} = (\vec{R}_1 - (\vec{e} \cdot \vec{R}_1) \vec{e})\cos\chi + (\vec{e} \times \vec{R}_1)\sin\chi + (\vec{e} \cdot \vec{R}_1) \vec{e}$

Приведя подобные, получим формулу поворота Родрига:

$\vec{R}_2 = (\vec{e} \cdot \vec{R}_1)(1-\cos\chi) \vec{e} + (\vec{e} \times \vec{R}_1)\sin\chi + \vec{R}_1 \cdot \cos \chi$

Литература

• Лурье А. И. Аналитическая механика. М.: ГИФМЛ, 1961. С. 101-103.