- Компьютерные шахматы
-
Эту страницу предлагается объединить с Шахматная программа. Пояснение причин и обсуждение — на странице Википедия:К объединению/20 декабря 2011.
Обсуждение длится одну неделю (или дольше, если оно идёт медленно).
Дата начала обсуждения — 2011-12-20.
Если обсуждение не требуется (очевидный случай), используйте другие шаблоны.
Не удаляйте шаблон до подведения итога обсуждения.Компьютерные шахматы — популярный термин из области исследования искусственного интеллекта, означающий создание программного обеспечения и специальных компьютеров для игры в шахматы. Также термин «компьютерные шахматы» употребляется для обозначения игры против компьютерной шахматной программы, игры программ между собой.
Содержание
История
История шахматных машин старше, чем история компьютеров. Идея создать машину, играющую в шахматы, датируется ещё восемнадцатым веком. Около 1769 года появился шахматный автомат «Механический турок». Он был предназначен для развлечения королевы Марии-Терезии. Машина действительно неплохо играла — внутри неё находился сильный шахматист, который и делал ходы.
Создание механических шахматных автоматов прекратилось с появлением цифровых компьютеров в середине XX века. В 1951 году Алан Тьюринг написал алгоритм, с помощью которого машина могла бы играть в шахматы, только в роли машины выступал сам изобретатель. Этот нонсенс даже получил название — «бумажная машина Тьюринга». Человеку требовалось более получаса, чтобы сделать один ход. Алгоритм был довольно условный, и сохранилась даже запись партии, где «бумажная машина» Тьюринга проиграла одному из его коллег[1]. За отсутствием доступа к компьютеру, программа ни разу не проверялась в работе.
Примерно в это же время, в 1951 году, математик Клод Шеннон написал свою первую статью о шахматном программировании. Он писал: «Хотя, возможно, это и не имеет никакого практического значения, сам вопрос представляется теоретически интересным, и будем надеяться, что решение этой задачи послужит толчком для решения других задач аналогичной природы и большего значения». Шеннон также отметил теоретическое существование лучшего хода в шахматах и практическую невозможность его найти.
Следующим шагом в развитии шахматного программирования стала разработка в ядерной лаборатории Лос-Аламоса в 1952 году на компьютере Maniac 1 (тактовая частота 11 кГц) шахматной программы для игры на доске 6x6, без участия слонов. Известно, что этот компьютер сыграл одну партию против сильного шахматиста, она продолжалась 10 часов и закончилась победой шахматиста. Ещё одна партия была сыграна против девушки, которая недавно научилась играть в шахматы. Машина победила на 23-м ходу. Сейчас это выглядит смешно, но для своего времени это было большое достижение.
В 1957 году Алексом Бернстейном была создана первая программа для игры на стандартной шахматной доске и при участии всех фигур[2].
Важное событие для компьютерных шахмат произошло в 1958 году, когда Аллен Ньюэлл, Клифф Шоу и Герберт Саймон разработали алгоритм уменьшения дерева поиска, названный Альфа-бета отсечение[2][3], на основе которого построены функции поиска всех сильных современных программ.
Первой же машиной, которая достигла уровня шахматного мастера, была Belle, законченная в 1983 г. Джо Кондоном и Кеном Томпсоном. «Belle» был первым компьютером, спроектированным только для игры в шахматы. Его официальный рейтинг Эло был 2250, таким образом, это была самая сильная шахматная машина своего времени.
В 1994 Гарри Каспаров проиграл программе Fritz 3 турнирную блиц-партию в Мюнхене. Программа также выиграла у Вишванатана Ананда, Бориса Гельфанда и Владимира Крамника. Гроссмейстер Роберт Хюбнер отказывался играть против программы и автоматически проиграл. Каспаров сыграл второй матч с Fritz и победил с 4 выигрышами и 2 ничьими.
В феврале 1996 года Гарри Каспаров победил шахматный суперкомпьютер Deep Blue со счетом 4-2. Этот матч выдающийся тем, что первую партию выиграл Deep Blue, автоматически став первым компьютером, победившим чемпиона мира по шахматам в турнирных условиях. Deep Blue вычислял 50 миллиардов позиций каждые три минуты, в то время как Каспаров 10 позиций за это же время. В Deep Blue было 200 процессоров. С тех пор шахматные энтузиасты и компьютерные инженеры создали много шахматных машин и компьютерных программ.
Шахматные компьютеры сейчас доступны по очень низкой цене. Появилось много программ с открытыми кодами, в частности Crafty, Fruit и GNU Chess, которые можно свободно загрузить из сети Интернет и которые могут победить многих профессиональных шахматистов. А лучшие коммерческие программы, например, Shredder или Fritz уже превысили уровень людей-чемпионов. Сейчас же движок Houdini находится на первом месте в таких компьютерных рейтинг-листах, как CEGT, CCRL,SCCT и CSS.
Мотивация
Первыми мотивами для компьютеризации шахмат было желание развлечься, создать программы для компьютерных шахматных турниров и провести научное исследование, которое позволило бы глубже понять познавательную способность человека. Для первых двух целей компьютерные шахматы имели феноменальный успех: от первых попыток к созданию шахматной программы, которая могла на равных соперничать с лучшими шахматистами, прошло менее пятидесяти лет.
А. С. Кронрод определил роль компьютерных шахмат известной фразой: «шахматы — это дрозофила искусственного интеллекта». Аналогия лежит на поверхности: шахматы представляют собой безусловно интеллектуальную, но при этом чётко формализованную, простую по структуре и компактную задачу, то есть являются удобным объектом лабораторных исследований в искусственном интеллекте, так же как мушка-дрозофила, благодаря малым размерам, плодовитости и быстрой смене поколений является удобным лабораторным объектом для изучения наследственности. Действительно, на шахматах были апробированы многие известные методы и направления искусственного интеллекта, в том числе методики оптимизации перебора (уход от «комбинаторного взрыва» при просчёте вариантов вперёд на несколько ходов), распознавание образов, экспертные системы, логическое программирование.
Однако, к удивлению и огорчению многих, шахматы мало приблизили людей к созданию машин с человекоподобным интеллектом. Современные шахматные программы, по сути, остановились на наиболее примитивном этапе интеллектуальной деятельности: они исследуют огромное число возможных ходов обоих игроков, применяя различные методы усечения дерева перебора, в том числе относительно простую функцию оценки. В сочетании с базами данных, хранящими заранее рассчитанные готовые варианты дебютов и эндшпилей, благодаря быстродействию и объёмам памяти современных компьютеров эти методы уже обеспечивают игру компьютера в шахматы на гроссмейстерском уровне. По этим причинам компьютерные шахматы больше не имеют такого большого академического интереса. Роль «дрозофилы искусственного интеллекта» перешла к другим интеллектуальным играм, таким как, например, го. Гораздо больший, чем в шахматах, объём перебора вариантов в таких играх ограничивает возможности использования простых методов и требует от ученых применять более умозрительные подходы к игре.
Проблемы реализации
Разработчики шахматных программы должны сделать ряд решений при их написании. Они включают:
- Способ изображения шахматной доски — представление цельной позиции как структуры данных.
- Методы поиска — поиск возможных лучших ходов.
- Листовая оценка — оценка позиции без учета дальнейших ходов.
См. также:
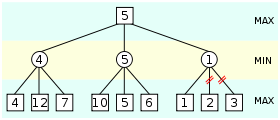
- Минимакс
- Альфа-бета отсечение
- Killer эвристика
- Итерационное заглубление
- Эвристика нулевого хода
Структура шахматной программы
Первое исследование на тему шахматного программирования сделал в 1950 году американский математик Клод Шеннон, успешно предусмотревший два основных возможных метода поиска, которые можно использовать, и назвал их «Тип А» и «Тип B».
Программы типа А используют так называемый подход «грубой силы» (brute force), изучая каждую возможную позицию на фиксированную глубину с помощью алгоритма Минимакс. Шеннон утверждал, что этот метод будет непрактичным по двум причинам.
Во-первых, с примерно тридцатью ходами, возможными в типичной позиции, на изучение около 10 млрд узловых позиций (просчет примерно на три хода вперед для обеих сторон), надо примерно 16 минут, даже в «очень оптимистичном» случае, когда компьютер сможет оценивать миллион позиций в секунду. (Чтобы достичь этого понадобилось сорок лет.)
Во-вторых, программы Типа А пренебрегали так называемой проблемой статического состояния, пытаясь оценить позицию в начале обмена фигур или другой важной последовательности ходов (например тактических комбинаций). Поэтому Шеннон предполагал, что с применением алгоритма Типа А число позиций, которые надо исследовать чрезвычайно возрастет, что значительно замедлит программу. Вместо бесполезной траты вычислительной мощности компьютера для исследования плохих или незначительных ходов Шеннон предложил использовать программы Типа В. Этот метод имеет два усовершенствования:
- Применяется поиск «по спокойствию» (quietness).
- Исследует не все, а только некоторые пригодные ходы для каждой позиции.
Это давало программам возможность просчитывать важные ходы на бо’льшую глубину и делать это за приемлемое время. Первый подход выдержал испытание временем: все современные программы применяют конечный поиск «по спокойствию» перед оценкой позиции.
Основные алгоритмы современных программ
Компьютерные шахматные программы рассматривают шахматные ходы как игровое дерево. Теоретически, они должны оценивать все позиции, которые возникнут после всех возможных ходов, затем все возможные ходы после этих ходов и т. д. Каждый ход одного игрока называется «узел». Перебор ходов продолжается, пока программа не достигает максимальной глубины поиска или определяет, что достигнута конечная позиция (например мат или пат). Уже на основании оценки позиции выбирает оптимальную стратегию. В каждой позиции количество возможных ходов игрока примерно равно 35. Для полного анализа четырёх ходов (по два хода каждого игрока) нужно исследовать около полутора миллиона возможностей, для шести — почти два миллиарда. Анализ на 3 хода вперед — очень мало для хорошей игры.
Программисты пытаются по-разному ограничить массу ходов, которые надо перебрать (обрезание дерева поиска — game tree pruning). Самым популярным является альфа-бета отсечение, в котором не рассматриваются позиции, имеющие меньшую оценку, чем уже оценённые.
Приблизительная программная реализация:
private int AlphaBeta(int color, int Depth, int alpha, int beta) { if (Depth == 0) return Evaluate(color); int bestmove; Vector moves = GenerateMoves(); for(int i = 0; i < moves.size(); i++) { makeMove(moves.get(i)); eval = -AlphaBeta(-color, Depth-1, -beta, -alpha); unmakeMove(moves.get(i)); if(eval >= beta) return beta; if(eval > alpha) { alpha = eval; if (Depth == defaultDepth) { bestmove = moves.get(i); } } } return alpha; }
Пример первого вызова:
AlphaBeta(1, 6, Integer.MIN_VALUE, Integer.MAX_VALUE);
При первом вызове метод (функция) вызывается с максимальным окном. При рекурсивных вызовах переменные alpha и beta меняются местами с инверсией знака и «сужают» массу поиска.
Вторым распространенным методом является итерационное заглубление. Сначала перебирается дерево игры до определенной глубины, после чего выделяется несколько лучших ходов. Затем программа оценивает эти ходы применительно к большей глубине, чтобы узнать больше об их последствиях. Эта операция повторяется до наилучшего с точки зрения программы хода. Такой подход позволяет быстро отбросить немалый процент неперспективных вариантов игры. Например, не имеет смысла исследовать, что произойдет, когда обменять ферзя на пешку, если в позиции есть лучшие ходы.
Важный элемент шахматных алгоритмов — это система оценки позиции. Нельзя абсолютно точно оценить позицию, ибо для этого нужно было бы проанализировать триллионы последовательностей ходов от начала и до завершения партии. Если бы существовала функция, которая давала бы возможность достоверно оценить позицию, задача игры в шахматы упростилась бы к оценке каждого из нескольких десятков доступных в данный момент ходов, и не надо было бы вычислять дальнейшие ходы.
Следовательно, оценка программой позиции очень приблизительная, хотя оценочные функции программ постоянно совершенствуются. Функции оценки обычно оценивают позиции в сотых частях пешки. Эти функции оценивают только несколько простых параметров:
- Во-первых, это оценка материала: каждая пешка — это 1 пункт, слон и конь — по 3, ладья — 5, ферзь — 9. Король иногда ценится в 200 пешек (Статья Шеннона) или 1 000 000 000 пешек (программа разработана в СССР в 1961 г.), чтобы гарантировать, что мат перевесит все другие факторы. Более развитые функции имеют точнее установленные коэффициенты ценности фигур, которые зависят от стадии партии и позиции на шахматной доске.
- Во-вторых, позиционное преимущество, которое зависит от положения фигур на доске; например, заблокированная фигура ценится меньше, чем свободная; оценивается также безопасность короля, господство над центром доски и т. д.; существуют также более сложные системы оценки (некоторые даже используют знания о нейронных сетях), однако даже такая простая функция позволяет программе играть очень сильно; в шахматах главная проблема заключается не в оценке позиции, а в переборе дерева возможных ходов.
Функции оценки позиции бывают неэффективны, когда ситуация на доске резко меняется с каждым ходом, когда, например, идёт обмен фигур или реализуется какая-нибудь шахматная комбинация. Отсюда возникло понятие статического состояния (quiescent) и горизонта вычисления. В статическом состоянии на шахматной доске идёт медленная позиционная борьба, а достойный внимания горизонт вычисления очень широк. Это означает, что решающая перемена не наступит в том будущем, которое удается легко предвидеть. В такой ситуации большую роль играют функции оценки позиции, нежели попытки вычисления возможных вариантов.
В динамичной ситуации игра, опирающаяся на функцию оценки позиции, может привести к совершенно ошибочным решениям. В крайнем случае, если программа имеет коротко настроенный горизонт исчисления и в ней учитывается только кратковременная оценка позиции, то конец может прийтись как раз на момент, когда идёт обмен ферзей, и один из них может быть уже побит, а второй взамен ещё нет. Оценка программой такого состояния ведёт к совершенно ошибочному выводу, что один из игроков имеет огромное преимущество, тогда как оно исчезнет через один ход, которого, однако, программа не видит. Если состояние ещё не статическое, нужно продолжить обмен до конца и оценить ситуацию, когда уже нет возможных радикальных изменений. Люди в целом интуитивно различают эти две ситуации — шахматные же программы должны иметь набор критериев, позволяющих изменять способ функционирования в статических и динамических состояниях.
Труднее дать оценку ходам в дебюте. Большинство программ используют при этом написанные заранее дебютные библиотеки, в которых есть определённое небольшое количество начальных ходов и ответов к определенному числу ходов, которое не является постоянным, потому что зависит от типа дебюта.
Компьютер против Человека
Даже в 70-80-х гг оставался открытым вопрос, когда шахматная программа сможет победить сильнейших шахматистов. В 1968 г. Международный гроссмейстер Дэвид Леви пошел на пари, что ни один компьютер не сможет обыграть его в течение ближайших десяти лет. Он выиграл пари, победив в 1978 г. программу Chess 4.7 (сильнейший в то время компьютер), но сознавал, что осталось не так уж много времени до того, когда компьютеры будут побеждать мировых чемпионов. В 1989 г. программа Deep Thought выиграла у Леви.
Но программы все еще были значительно ниже уровня Чемпиона мира, который продемонстрировал Гарри Каспаров, победив ту же Deep Thought дважды в 1991 г.
Это длилось до 1996 г., когда состоялся матч Каспарова с компьютером Deep Blue фирмы IBM, где чемпион проиграл свою первую партию. Впервые компьютерная шахматная программа обыграла чемпиона мира при стандартном часовом контроле. Однако Каспаров изменил свой стиль игры, выиграв три и сведя вничью две из пяти партий, которые остались.
В мае 1997 года усовершенствованная версия Deep Blue нанесла поражение Каспарову со счетом 3,5-2,5. Позже IBM обвинили, что во время партий фирма использовала человека-шахматиста, чтобы увеличить стратегическую силу компьютера.
В 2003 году был снят документальный фильм, в котором исследовались эти упреки, который называется «Матч окончен: Каспаров и машина» (англ. Game Over: Kasparov and the machine), в котором утверждалось, что сильно раскрученная победа Deep Blue подстроена для увеличения рыночной стоимости IBM.
Частично эти упреки были оправданными. Правила позволяли разработчикам изменять программу между играми. Deep Blue был изменен между партиями для лучшего понимания машиной стиля игры Каспарова, помогая избежать ловушки в эндшпиле, в которую дважды попадал искусственный интеллект.
IBM разобрала Deep Blue после матча, с тех пор этот компьютер не играл ни разу. Хотя происходили другие матчи «Человек против Машины».
Имея все большую вычислительную мощность, шахматные программы, запущенные на персональных компьютерах, стали достигать уровня лучших шахматистов. В 1998 г. программа Rebel 10 победила Вишванатана Ананда, который тогда занимал второе место в мире. Однако не все партии игрались со стандартным временным контролем. Из восьми партий матча, четыре играли с блиц-контролем (пять минут плюс пять секунд за каждый ход), которые Rebel выиграл со счетом 3-1. Еще две игры были с полу-блиц контролем (пятнадцать минут на каждого), которые программа также выиграла (1,5-1). Наконец, две последние партии были сыграны со стандартным турнирным временным контролем (два часа на 40 ходов и час на остальные партии) и тут выиграл уже Ананд со счетом 0,5-1,5. К тому времени в быстрых партиях компьютеры играли лучше людей, но при классическом временном контроле преимущество было уже не так велико.
В 2000 г. коммерческие шахматные программы Junior и Fritz смогли свести в ничью матчи против предыдущих мировых чемпионов Гарри Каспарова и Владимира Крамника.
В октябре 2002 Владимир Крамник и Deep Fritz соревновались в матче из восьми партий в Бахрейне. Матч закончился вничью. Крамник выиграл вторую и третью партии, используя традиционную противокомпьютерную тактику — играл осторожно, имея целью долгосрочное преимущество, которое компьютер не может увидеть в своем дереве поиска. И все же Fritz выиграл пятую партию после грубой ошибки Крамника. Шестую партию много турнирных комментаторов назвали очень увлекательной. Крамник, имея лучшую позицию в начале миттельшпиля, попытался пожертвовать фигурой, чтобы создать сильную тактическую атаку (такая стратегия — очень рискованная против компьютеров). Fritz нашел сильную защиту, и эта атака значительно ухудшила позицию Крамника. Крамник сдал игру, веря, что партия проиграна. Однако последующий анализ показал, что Fritz вряд ли смог бы довести игру до своего выигрыша. Последние две партии закончились вничью.
В январе 2003 г. Гарри Каспаров играл против программы Junior в Нью-Йорке. Матч закончился со счетом 3-3.
В ноябре 2003, Гарри Каспаров играл с X3D Fritz. Матч закончился со счетом 2-2.
В 2005 г., Hydra, специальный шахматный компьютер с 64 процессорами, победил Майкла Адамса, шахматиста, который в то время был на седьмом месте в мире по рейтингу ЭЛО, в матче из шести партий со счетом 5,5-0,5 (хотя домашняя подготовка Адамса была намного ниже, чем у Каспарова в 2002 году). Некоторые комментаторы верили, что Hydra наконец получит несомненное преимущество над лучшими шахматистами.
В ноябре-декабре 2006, Владимир Крамник играл с программой Deep Fritz. Матч закончился со счетом 2-4.
Базы данных эндшпиля
Подробнее Базы данных эндшпиля
Компьютеры используются для анализа некоторых эндшпильных позиций. Такие базы данных эндшпиля создаются, используя ретроградный анализ, начиная с позиций, где конечный результат известен (например, где одной стороне был поставлен мат) и видя какие еще позиции есть на расстоянии хода, затем на один ход от этих и т. д. Кен Томпсон, известный как главный проектировщик операционной системы UNIX, был пионером в этой области.
Игра в эндшпиле долго была заметной слабостью шахматных программ, так как глубина поиска была недостаточной. Таким образом, даже программы, которые играли в силу мастера не в состоянии выиграть в эндшпильних позициях, где даже шахматист средней силы мог форсировать выигрыш.
Но результаты компьютерного анализа иногда удивляли людей. В 1977 г. шахматная машина Томпсона Belle, используя эндшпильные базы данных король + ладья против короля + ферзь, была способна свести вничью теоретически проигрышные эндшпили против титулованных шахматистов.
Большинство гроссмейстеров отказывались играть против компьютера в эндшпиле ферзь против ладьи, но Уолтер Браун принял вызов. Позицию расставили так, что теоретически можно было выиграть в 30 ходов с безупречной игрой. Брауну дали два с половиной часа на пятьдесят ходов. После сорока пяти ходов Браун согласился на ничью, будучи не способным выиграть в последние пять ходов. В конечной позиции, Браун мог поставить мат только через семнадцать ходов.
В 2002 г. были опубликованы основные форматы эндшпильных баз данных, включая Edward Tablebases, De Koning Endgame Database и Nalimov Endgame Tablebases, которые теперь поддерживают многие шахматные программы, такие как Rybka, Shredder и Fritz. Эндшпили с пятью или менее фигурами были полностью проанализированы. Эндшпили с шестью фигурами были проанализированы, за исключением позиций с пятью фигурами против одинокого короля. Марк Буржуцкий и Яков Коновал проанализировали некоторые эндшпили с семью фигурами. Во всех этих эндшпильных базах данных считается, что рокировка невозможна.
Базы данных генерируются с помощью хранения в памяти оценок позиций, которые возникали до сих пор, и используют этих результаты для уменьшения дерева поиска, если такие позиции возникнут снова. Простая целесообразность запоминания оценок всех ранее достигнутых позиций означает, что ограничивающим фактором при решении эндшпиля является просто количество памяти, которую имеет компьютер. С ростом ёмкости компьютерной памяти, эндшпили повышенной сложности рано или поздно будут решены.
Компьютер, использующий базу данных эндшпиля будет, при достижении позиции в них, способен играть безупречно и безотлагательно определять, является ли позиция выигрышной, проигрышной или ничейной, а также находить самый быстрый и самый долгий способ достижения результата. Знание точной оценки позиции также полезно при увеличении силы компьютера, так как это позволит программе выбирать пути достижения цели в зависимости от ситуации [то есть упрощая и размениваясь получить четко исследованную позицию].
Базы эндшпиля Налимова на пять фигур, которые используют методы современной компрессии, занимают 7.05 Гб на жестком диске. Для хранения баз данных на шесть фигур надо примерно 1.2 терабайт. Оценено, что полная семифигурная база данных потребует больше места, чем будет доступно рядовым пользователям в ближайшем будущем.
Игра против программ
Компьютеры ощутимо опережают людей в коротких тактических маневрах, которые находятся в пределах глубины поиска программы. Особенно опасным в таких случаях является ферзь, который прекрасно подходит для кратковременных маневров. Поэтому в игре против компьютера люди часто делают попытку побудить программу к размену ферзей. Это происходит, например, когда человек в начале партии намеренно ухудшает свою позицию, а компьютер расценивает её, как выгодную ему. Если программа устанавливает оценку позиции как преимущественную для себя, то, скорее всего, будет разменивать фигуры, а это выгодно человеку. Конечно, программисты узнали о таких «трюках», и это учитывается в последних версиях их программ.
Вместо этого шахматисты должны играть против компьютера долгосрочными маневрами, которые программа не может увидеть в рамках своей глубины поиска. Например, Крамник в партии с Deep Fritz выиграл с помощью долгосрочного продвижения проходной пешки, которую Fritz обнаружил слишком поздно.
Шахматы и другие игры
Успех шахматных программ внушает мысль, что можно написать программы, которые играли бы так же хорошо и в другие игры, например сёги или го.
Похожие алгоритмы, пожалуй, можно бы использовать и во время игры в других разновидностях шахмат. В сёги больше возможных ходов, материальное преимущество значит гораздо меньше, зато намного существеннее позиционное преимущество. Строятся сложные системы, имеющие целью гарантировать королю безопасность, но оценка этих систем для компьютера нелегка. Количество фигур в этой игре постоянно, а потому игра не упрощается со временем, что делает невозможным создать базу эндшпилей. Нет здесь также вполне статических состояний, ведь игра на протяжении всего времени сводится к позиционной борьбе. Поэтому написать хорошую программу для игры в сёги значительно тяжелее, чем шахматную программу, хотя огромный опыт в шахматных играх можно приложить и к этой игре.
Настоящим вызовом для программистов стало го. Сложность вычисления го на несколько порядков больше, чем в шахматах. На каждом шаге возможны около 200—300 ходов, статическая же оценка жизни групп пешек фактически невозможна. Одним ходом здесь можно вполне испортить всю игру, даже если остальные ходы были успешны. Поэтому программы для игры в го не используют таких алгоритмов, как шахматные программы, и обычно имеют несколько десятков модулей для оценки различных аспектов игры и при анализе пытаются пользоваться теми же понятиями, что и люди. Несмотря на это, компьютеры в го играют еще очень слабо и проигрывают даже не очень сильным любителям.
Хронология компьютерных шахмат
- 1769, Вольфганг Кемпелен, построил шахматиста-автомата, который стал одной из величайших мистификаций этого периода.
- 1868, Чарльз Хупер представил автомат Ajeeb — в котором тоже был спрятан шахматист.
- 1912, Леонардо Торрес Квеведо построил машину, которая могла играть эндшпиле Король + Ладья против короля.
- 1948, книга Норберта Винера «Кибернетика» описывает, как можно создать шахматную программу, используя поиск минимакса с лимитированной глубиной и оценочной функцией.
- 1950, Клод Шеннон опубликовал «Программирование компьютера для игры в шахматы», одну из первых статей о компьютерных шахматах.
- 1951, Алан Тьюринг разработал на бумаге первую программу, способную играть в шахматы.
- 1952, Дитрих Принц разработал программу, которая решала шахматные задачи.
- 1956, г. Лос-Аламос — первая подобная шахматам игра, которую смогли играть программы, разработанная Полом Штейном и Марком Уэллсом для компьютера MANIAC I.
- 1956, Джон Маккарти изобрел альфа-бета алгоритм поиска.
- 1958, NSS стала первой программой, которая использовала альфа-бета алгоритм поиска.
- 1958, первыми шахматными программами, которые могли играть полные шахматные партии, стали одна, созданная Алексом Бернштайн и вторая российскими программистами.
- 1962, первой программой, которая играла правдоподобно стала Kotok-McCarthy.
- 1966—1967, первый матч между программами.
- 1967, Mac Hack Six, разработанная Ричардом Гринблатт стала первой программой, победившей человека при турнирном контроле времени.
- 1970, первый год Североамериканского Компьютерного Шахматного Чемпионата.
- 1974, Каисса выиграла первый Всемирный Компьютерный Шахматный Чемпионат.
- 1977, создана первая шахматная программа для микрокомпьютеров CHESS CHALLENGER.
- 1977, создание Международной Компьютерной Шахматной Ассоциации.
- 1977, Chess 4.6 стал первым шахматным компьютером, который добился успеха в главном шахматном турнире.
- 1980, первый год Всемирного микрокомпьютерного Шахматного Чемпионата.
- 1981, Cray Blitz выиграл Чемпионат Штата Миссисипи с 5-0 счетом и рейтингом производительности 2258.
- 1982, аппаратный шахматный игрок Кена Томпсона Belle зарабатывает титул мастера США.
- 1988, HiTech, разработанная Гансом Берлинером и Карлом Ебелингом, выигрывает матч против гроссмейстера Арнольда Денкер со счетом 3.5 — 0.5.
- 1988, Deep Thought делит первое место с Тони Майлзом в Чемпионате ПО Toolworks, впереди бывшего чемпиона мира Михаила Таля и нескольких гроссмейстеров, в частности Самуэля Решевского, Уолтера Брауна, Эрнста Грюнфельда и Михаила Гуревича. Программа также нанесла поражения гроссмейстер Бенту Ларсену, и стала первым компьютером, который выиграл у гроссмейстера в турнире.
- 1992, впервые микрокомпьютер, Chessmachine Gideon 3.1, разработанный Эдом Шредером (Ed Schröder) выигрывает VII Всемирный Компьютерный Шахматный Чемпионат впереди суперкомпьютеров.
- 1997, Deep Blue выиграл матч против Гарри Каспарова 2-1 = 3.
- 2002, Владимир Крамник свел вничью матч против Deep Fritz.
- 2003, Каспаров сыграл вничью матч против Deep Junior.
- 2003, Каспаров сыграл вничью матч против X3D Fritz.
- 2005, Hydra выиграла матч с Майклом Адамсом со счетом 5,5-0,5.
- 2005, команда компьютеров (Hydra, Deep Junior и Fritz), обыграла 8.5-3.5 команду из шахматистов (Веселин Топалов, Руслан Пономарев и Сергей Карякин), которые имели средний ЭЛО рейтинг 2681.
- 2006, чемпион мира, Владимир Крамник, побежден 4-2 Deep Fritz.
Теоретики компьютерных шахмат
- Дэвид Леви
- Роберт Хайатт (автор шахматной программы Crafty)
- Ганс Берлинер
- Клод Шеннон
- Давид Бронштейн
См. также
Примечания
- ↑ Alan Turing vs Alick Glennie // «Turing Test», 1952
- ↑ 1 2 Early Computer Chess Programs // Bill Wall’s Wonderful World of Chess
- ↑ Computer Chess History by Bill Wall
Ссылки
- История компьютерных шахмат
- Защита Чести Человечества — статья Тима Краббе об «антикомпьютерном» стиле шахмат
- Computer-Chess Club — место, где профессиональные авторы обсуждают свои программы
- Компьютерная шахматная теория Колина Фрауна
Шахматы История · Правила · Дебюты · Стратегия · Тактика · Эндшпиль · Чемпионаты мира · Турниры · Компьютеры · Варианты Категория:- Компьютерные шахматы
Wikimedia Foundation. 2010.