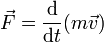Центростремительная и центробежная силы

Центростремительная и центробежная силы

Центростремительная и центробежная силы

Классическая механика

$\vec{F} = \frac{\mathrm{d}}{\mathrm{d}t}(m \vec{v})$ Второй закон Ньютона

История… Фундаментальные понятия Пространство · Время · Масса · Сила Энергия · Импульс Формулировки Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби Разделы Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика Учёные Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши

В буквальном смысле эти силы выглядят как определённым способом ориентированные по отношению к центру — некой точке, равноудалённой от всех точек траектории движущегося тела. В двумерном пространстве (на плоскости) такой траекторией является окружность, а в трехмерном — тоже окружность, образованная пересечением сферической поверхности плоскостью, в общем случае не проходящей через её центр.
Все остальные траектории любого вида центром в этом смысле не обладают, и потому применительно к движущемуся по не круговым траекториям телу использование представления о центростремительной и центробежной силах не оправдано и ведёт к многочисленным недомолвкам и недоразумениям.

Центростремительная и центробежная силы

Центростремительная сила — сила, действующая со стороны неких связей, ограничивающих свободу движения тела, и вызывающая его поворот вокруг центра поворота. Природа связей может быть любой, если они обладают свойством увеличивать потенциальную энергию системы тело-связь при удлинении последней.

Реально существующей является лишь сила реакции связи. Центростремительная, равно как и центробежная сила, как самостоятельная сила, не существует и представляет собой лишь результат формального разложения реальной силы на две составляющие.

В случае установившегося движения тела (вращения) центростремительная сила совпадает с силой, представляющей собой реакцию связи , она направлена перпендикулярно к вектору его скорости, работы не совершает, кинетическая энергия движения тела не изменяется и такое движение может продолжаться неограниченно долго.

В случае неустановившегося движения по кривой (например при раскрутке пращи), траектория движения тела представляет собой спираль и центростремительная сила, по определению нормальная по касательной к траектории, направлена в сторону мгновенного центра вращения и представляет собой результат формального разложения реальной силы реакции связи на две. При этом работу совершает тангенциальная составляющая силы реакции связи, ведущая к изменению кинетической энергии тела (при разгоне) или уменьшению её (при торможении). Это периодически имеет место в Мировом пространстве при движении небесных дел по кеплеровским эллиптическим орбитам вокруг общего центра тяготения

Центробе́жная си́ла — сила, действующая со стороны испытывающего поворот тела на вызывающие этот поворот связи, равная по модулю центростремительной силе и всегда направленная в противоположную ей сторону (Третий закон Ньютона). Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин Центробежная сила (букв. Сила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющего его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона) ^[1] в форме :

Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы

Или ещё^[2]:

Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.

Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так. ^[3]

Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной формы его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Нютон связывал её с эфиром, заполняющим всё пространство)^[4], остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.

Рассматриваемое тело с массой (точнее — инертной массой) m приобретает отличающееся от нуля ускорение a в тот же момент t = 0, когда начинает действовать на него сила F. (Второй закон Ньютона :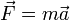$\vec F = m \vec a$) Однако для достижения отличающейся от нуля скорости v требуется некоторое время t в соответствие с определением импульса силы : t = mv / F .Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила. ^[5]

Использование термина Центробежная сила правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле Центробежная сила представляет собой один из членов в формулировке Третьего закона Ньютона, антагониста Центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направление движения тела (материальной точки).

Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины M₁ и M₂, находящихся на расстоянии R друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и R есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения F_G:GM₁M₂ / R², где G- гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями v₁ = ω₁ R₁ и v₂ = ω₂ R₂, то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: ω₁ = ω₂ = ω, а расстояния от центра вращения (центра масс) будут соотноситься, как: M₁ / M₂ = R₂ / R₁, причём R₂ + R₁ = R, что непоcредственно следует из равенства действующих сил: F₁ = M₁a₁ и F₂ = M₂a₂, где ускорения равняются соответственно: a₁= ω²R₁ и a₂ = ω²R₂ ^[6]

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): F₁ =F₂ = F_G . При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствие с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы Всемирного тяготения. То же самое справедливо и отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

Переписывая Второй закон в виде F − ma = 0 и заменяя второй член слева на некую силу F_i = − ma, получаем новую запись Второго закона: F + F_i = 0.Здесь обе силы действуют на одно и то же тело, причём их сумма равна нулю, из чего следует, что данное тело в системе отсчёта, связанной с этим телом, покоится, хотя сама система вместе с ним движется ускоренно. Эта сила F_i, ничем не отличается по своему происхождению от силы F (о чём говорит знак равенства в канонической записи закона). Существует предложение называть её Ньютоновской силой инерции. Никакого отношения к центробежной силе эта сила не имеет. ^[5]

Литература

• Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
  
• С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
  
• Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. М.: ГИТТЛ, 1957
  
• «Центробежная сила» в Большой советской энциклопедии

См. также

• Сила Кориолиса
• Закон инерции

Примечания

1. ↑ Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
2. ↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей . Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
3. ↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким апеллируя к тому, что оно становится сладким не само по себе, а лишь после того, что в него положен сахар.
4. ↑ Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
5. ↑ ^{1 2} С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
6. ↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Связать^?