- Тест Соловея — Штрассена
-
Тест Соловея — Штрассена
Тест Соловея — Штрассена — вероятностный тест простоты, открытый в 1970-х годах Робертом Мартином Соловеем совместно с Фолькером Штрассеном.[1] Тест всегда корректно определяет, что простое число является простым, но для составных чисел с некоторой вероятностью он может дать неверный ответ. Основное преимущество теста заключается в том, что он не «реагирует» и отсеивает как составные числа Кармайкла, на которых всегда ошибается тест Ферма.
Содержание
Псевдопростые числа
Натуральное n
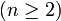 называется псевдопростым по основанию a, где
называется псевдопростым по основанию a, где 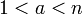 , если a и n взаимнопросты, и
, если a и n взаимнопросты, и 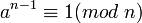 .
.Нечетное составное число m называется псевдопростым эйлеровым числом по основанию w, если оно удовлетворяет сравнению
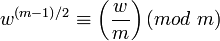 , где
, где 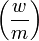 есть символ Лежандра.
есть символ Лежандра.Так как из сравнения
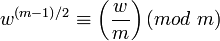 следует, что
следует, что 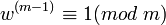 , то псевдопростое эйлерово число по основанию w так же является псевдопростым числом по основанию w.
, то псевдопростое эйлерово число по основанию w так же является псевдопростым числом по основанию w.Тест Соловея — Штрассена
Тест Соловея — Штрассена опирается на малую теорему Ферма и свойства символа Лежандра. Основан на следующем утверждении:
- Если m — нечетное составное число, то количество целых чисел w, взаимнопростых с m, удовлетворяющих сравнению
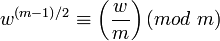 и таких, что
и таких, что 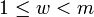 , не превосходит
, не превосходит 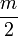 .
.
Алгоритм Соловея — Штрассена
Алгоритм Соловея — Штрассена параметризуется количеством раундов k. В каждом раунде случайным образом выбирается число w < m. Если (w,m) > 1, то выносится решение, что m составное. Иначе проверяется справедливость сравнения
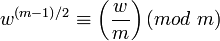 . Если оно не выполняется, то выносится решение, что m - составное. Если это сравнение верно, то w является свидетелем простоты m. Далее выбирается другое случайное w и процедура повторяется. После нахождения k свидетелей простоты в k раундах на основании вышеприведенного утверждения выносится заключение, что m с вероятностью
. Если оно не выполняется, то выносится решение, что m - составное. Если это сравнение верно, то w является свидетелем простоты m. Далее выбирается другое случайное w и процедура повторяется. После нахождения k свидетелей простоты в k раундах на основании вышеприведенного утверждения выносится заключение, что m с вероятностью 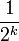 является простым числом.
является простым числом.На псевдокоде алгоритм может быть записан следующим образом:
Вход: m > 2, нечётное натуральное число, которое необходимо проверить на простоту; k, параметр, определяющий точность теста. Выход: составное, означает, что m точно составное; вероятно простое, означает, что m вероятно является простым. for i = 1, 2, ..., k: w = случайное целое от 2 до m − 1, включительно; если НОД(w, m) > 1, тогда: вывести, что m — составное, и остановиться. если
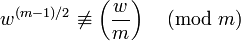 , тогда:
вывести, что m — составное, и остановиться.
вывести, что m — вероятно простое, и остановиться.
, тогда:
вывести, что m — составное, и остановиться.
вывести, что m — вероятно простое, и остановиться.
Вычислительная сложность и точность
На каждой итерации алгоритма составное число может быть распознано с вероятностью не менее 1 / 2. После k независимых итераций, эта вероятность составляет 2 − k.
Эта степень надежности теста Соловея — Штрассена иногда признается неудовлетворительной,[2] так как, например, более новый тест Миллера — Рабина достигает вероятности ошибки не более 4 - k после k итераций алгоритма.
Алгоритм требует O(klog2n) операций над длинными целыми числами.[1]
Примечания
- ↑ 1 2 Solovay, Robert M. and Volker Strassen (1977, submitted in 1974). «A fast Monte-Carlo test for primality». SIAM Journal on Computing 6 (1): 84–85. DOI:10.1137/0206006.
- ↑ http://www.vntr.ru/ftpgetfile.php?id=323
Литература
- Н. Коблиц. Курс теории чисел и криптографии. — ISBN 5-94057-103-4
Ссылки
- http://www.ssl.stu.neva.ru/psw/crypto/open_key_crypt.pdf
- http://gultyaeva.sdbe.ami.nstu.ru/fti&c/Materials/lr_fti&c.pdf
Wikimedia Foundation. 2010.
- Если m — нечетное составное число, то количество целых чисел w, взаимнопростых с m, удовлетворяющих сравнению
Тест Соловея — Штрассена вероятностный тест простоты, открытый в 1970 х годах Робертом Мартином Соловеем совместно с Фолькером Штрассеном.[1] Тест всегда корректно определяет, что простое число является простым, но для составных чисел с некоторой вероятностью… … Википедия
Тест простоты — Тест простоты алгоритм, который по заданному натуральному числу определяет, простое ли это число. Различают детерминированные и вероятностные тесты. Определение простоты заданного числа в общем случае не такая уж тривиальная задача. Только… … Википедия
Тест Ферма — Тест простоты Ферма в теории чисел это тест простоты натурального числа n, основанный на малой теореме Ферма. Содержание Если n простое число, то оно удовлетворяет сравнению для любого a, где n не делит a. Выполнение сравнения… … Википедия
Тест Миллера (теория чисел) — У этого термина существуют и другие значения, см. Тест Миллера. Не следует путать с «Тестом Миллера Рабина» вероятностным полиномиальным тестом простоты. Тест Миллера детерминированный полиномиальный тест простоты. В 1976 году Миллер… … Википедия
Тест простоты Люка — В теории чисел тест простоты Люка это тест простоты натурального числа n; для его работы необходимо знать разложение на множители. Для простого числа n простые множители числа вместе с некоторым основанием a составляют сертификат Пратта, который… … Википедия
Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия
Программируемые алгоритмы — Служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавл … Википедия
Критерий Поклингтона — детерминированный тест на простоту. Критерий Поклингтона позволяет определять, является ли простым данное число. Содержание 1 Теорема Поклингтона 2 Доказательство теоремы Поклингто … Википедия
Псевдопростое число — Натуральное число называется псевдопростым, если оно обладает некоторыми свойствами простых чисел, являясь тем не менее составным числом. В зависимости от рассматриваемых свойств существует несколько различных типов псевдопростых чисел.… … Википедия
