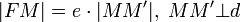Эксцентричность орбиты

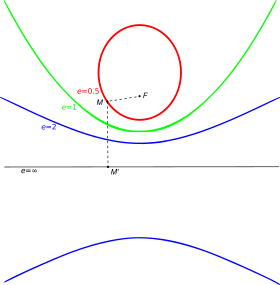Эллипс (e=1/2), парабола (e=1) и гипербола (e=2) с фиксированными фокусом F и директрисой. (|FM| = e |MM'|)

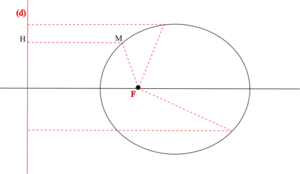Эллипс и его e = 1 / 2

Эксцентрисите́т (обозначается “e” или “ε”) — числовая характеристика конического сечения, показывающая степень его отклонения от окружности.

Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия.

Определение

Все невырожденные конические сечения, кроме окружности, можно описать следующим способом:

Выберем на плоскости точку F и прямую d и зададим вещественное число e > 0. Тогда геометрическое место точек, для которых расстояние до точки F и до прямой d отличается в e раз, является коническим сечением. Точка F называется фокусом конического сечения, прямая d — директрисой, число e — эксцентриситетом.

$|FM| = e\cdot |MM'|,\ MM' \bot d$

В зависимости от эксцентриситета, получится:

• при e > 1 — гипербола.
• при e = 1 — парабола;
• при e < 1 — эллипс;

Другие определения

Эллипс и оси

Для окружности полагают e = 0, так как для эллипса эксцентриситет ещё можно определить через отношение большой (a) и малой (b) полуосей: e² = 1 − b² / a². При e = 0 кривая круговая (полуоси равны), при 0 < e < 1 - эллиптическая.

Так же для эллипса и гиперболы эксцентриситет ещё можно определить как отношение расстояний между фокусами к большей или действительной оси.

Литература

• А. В. Акопян, А. А. Заславский Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136с.