Цикл Эйлера

Граф Кёнигсбергских мостов. Этот граф не является эйлеровым, поэтому решения не существует.

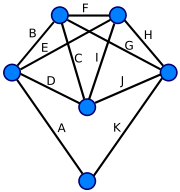Каждая вершина этого графа имеет чётную степень, поэтому этот граф — эйлеров. Обход рёбер в алфавитном порядке даёт эйлеров цикл.

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Эйлеров граф — граф, содержащий эйлеров цикл.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

Существование эйлерова цикла и эйлерова пути

Разумеется, эйлеров цикл/путь существуют только в связных графах или в графах, которые после удаления всех одиночных вершин превратятся в связные.

В неориентированном графе

Кроме того, согласно теореме, доказанной Эйлером, эйлеров цикл существует тогда и только тогда, когда в графе отсутствуют вершины нечётной степени. Эйлеров путь существует тогда и только тогда, когда число вершин нечётной степени не превосходит двух.

Теорема: Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечётной степени.^[1][2]

В ориентированном графе

Связный ориентированный граф содержит эйлеров цикл тогда и только тогда, когда для каждой вершины графа её полустепень захода равна её полустепени исхода, то есть в вершину входит столько же ребер, сколько из нее и выходит.

Поиск эйлерова пути в графе

Можно всегда свести задачу поиска эйлерова пути к задаче поиска эйлерова цикла. Действительно, предположим, что эйлерова цикла не существует, а эйлеров путь существует. Тогда в графе будет ровно 2 вершины нечётной степени. Соединим эти вершины ребром, и получим граф, в котором все вершины чётной степени, и эйлеров цикл в нём существует. Найдём в этом графе эйлеров цикл (алгоритмом, описанным ниже), а затем удалим из ответа несуществуещее ребро.

Поиск эйлерова цикла в графе

Будем рассматривать самый общий случай — случай ориентированного мультиграфа, возможно, с петлями. Также мы предполагаем, что эйлеров цикл в графе существует (и состоит хотя бы из одной вершины). Для поиска эйлерова цикла воспользуемся тем, что эйлеров цикл — это объединение всех простых циклов графа. Следовательно, наша задача — эффективно найти все циклы и эффективно объединить их в один.

Реализовать это можно, например, так, рекурсивно:

procedure find_all_cycles (v)
var массив cycles
1. пока есть цикл, проходящий через v, находим его
    добавляем все вершины найденного цикла в массив cycles (сохраняя порядок обхода)
    удаляем цикл из графа
2. идем по элементам массива cycles
    каждый элемент cycles[i] добавляем к ответу
    из каждого элемента рекурсивно вызываем себя: find_all_cycles (cycles[i])

Достаточно вызвать эту процедуру из любой неодиночной вершины графа, и она найдёт все циклы в графе, удалит их из графа и объединит их в один эйлеров цикл.

Для поиска цикла на шаге 1 используем поиск в глубину.

Сложность полученного алгоритма — O(M), то есть линейная относительно количества рёбер М в данном графе.

Пример реализации на C++

#include <stdio.h>
#include <vector>
using namespace std;
 
vector <int> eulerCycle,cycle;
int  a[100][100],n,b[100][100];
 
bool dfs (int i) {
	cycle.push_back(i);
	if (cycle.size() > 1 && i==cycle[0])
		return true;
 
	for (unsigned j=1; j<=n; ++j)
		if (a[i][j]) {
			--a[i][j];
			//--a[j][i];
			if (dfs (j)) return true;
		}
	cycle.pop_back();
	return false;
}
 
void findCycles (int i) {
	vector<int> cycles;
 
	for (;;) {
		memcpy (b,a,sizeof(a));
		cycle.clear();
		if (!dfs (i)) break;
		memcpy (a,b,sizeof(b));
 
		for (unsigned j=0; j<cycle.size()-1; ++j) {
			cycles.push_back (cycle[j+1]);
			--a[cycle[j]][cycle[j+1]];
			--a[cycle[j+1]][cycle[j]];
		}
	}
 
	for (unsigned j=0; j<cycles.size(); ++j) {
		eulerCycle.push_back (cycles[j]);
		findCycles (cycles[j]);
	}
}
 
int main () {
        unsigned m;
	scanf ("%d %u",&n,&m);
	while (m--) {
                unsigned i,j;
		scanf ("%d %d",&i,&j);
		a[i][j] = /*a[j][i] =*/ 1;
	}
 
	eulerCycle.push_back (1);
	findCycles (1);
 
	for (unsigned i=0; i<eulerCycle.size(); ++i)
		printf (" %d", eulerCycle[i]);
        printf ("\n");
 
	system ("pause");
	return 0;
}

Примечания

1. ↑ Эйлеровы пути
2. ↑ Маршруты и связность в орграфах

См. также

• Гамильтонов цикл
• Граф (математика)
• Задача о ходе коня
• Дискретная математика
• Семь мостов Кёнигсберга
• Список объектов, названных в честь Леонарда Эйлера

Ссылки

• Реализация алгоритма поиска эйлерова цикла (краткие описания и программы на C++)
• Реализация алгоритма поиска эйлерова цикла на codenet.ru
• Теория графов и комбинаторика
• Эйлеровы и Гамильтоновы графы
• Графы. Циклы и разрезы (ДИСКРЕТНАЯ МАТЕМАТИКА: АЛГОРИТМЫ, Визуализаторы)
• Е. Гик. «Шахматы и математика» Конь-хамелеон
• Weisstein, Eric W. Eulerian Circuit на сайте Wolfram MathWorld.(англ.)