Цикл де Брюина

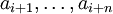Последовательность де Бре́йна^[1] — последовательность $a_1,\dots,a_t$, элементы которой принадлежат заданному конечному множеству (обычно рассматривают множество $\lbrace0,1,\dots,k-1\rbrace$) и все подпоследовательности $a_{i+1},\dots,a_{i+n}$ заданной длины n различны.

Часто рассматриваются периодические последовательности с периодом T, содержащие T различных подпоследовательностей 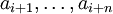$a_{i+1},\dots,a_{i+n}$ — то есть такие периодические последовательности, в которых любой отрезок длины T + n − 1 является последовательностью де Брейна с теми же параметрами n и k.

Очевидно, что длина (период) такого цикла не может превосходить числа kⁿ всех различных векторов длины n с элементами из $\lbrace0,1,\dots,k-1\rbrace$; несложно доказать, что эта оценка достигается. Циклы этой максимально возможной длины обычно называют циклами де Брейна (впрочем, иногда этот термин применяют и к циклам меньшей длины).

Примеры циклов де Брейна для k = 2 с периодом 2, 4, 8, 16:

• 01 (содержит подпоследовательности 0 и 1)
• 0011 (содержит подпоследовательности 00, 01, 11, 10)
• 00010111 (000, 001, 010, 101, 011, 111, 110, 100)
• 0000100110101111

Циклы де Брейна названы по имени голландского математика Н. Г. де Брёйна (Nicolaas Govert de Bruijn), который рассматривал их в 1946 году^[2], хотя они изучались и ранее^[3].

Число циклов де Брейна с параметрами n и k есть $k!^{k^{(n - 1)}}/k^n$ (частный случай теоремы де Брейна — Эренфест — Смита — Тутте, «BEST-theorem»).

Существует удобная интерпретация последовательностей и циклов де Брейна, основанная на так называемом графе де Брейна — ориентированном графе с kⁿ вершинами, соответствующими kⁿ различных наборов длины n с элементами из 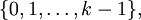$\lbrace0,1,\dots,k-1\rbrace,$ в котором из вершины 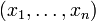$(x_1,\dots,x_n)$ в вершину $(y_1,\dots,y_n)$ ребро ведет в том и только том случае, когда $\,x_i = y_{i-1},$ $i=2,\dots,n;$ при этом самому ребру можно сопоставить набор длины n+1: $(x_1,\dots,x_n,y_n)=(x_1,y_1,\dots,y_n).$ Для такого графа не проходящие дважды через одно и то же ребро пути (циклы) соответствуют последовательности (циклу) де Брейна с параметрами n+1 и k, а не проходящие дважды через одну и ту же вершину пути (циклы) — последовательности (циклу) де Брейна с параметрами n и k.

При k = 2 существуют такие циклы де Брейна с длиной, на единицу меньшей максимума, которые выражаются линейными рекуррентными соотношениями порядка n: так, при n = 3 соотношение $\,x_n = x_{n-2}+x_{n-3} \pmod 2$ порождает последовательности с периодом 7, например 0010111001011100... (цикл де Брейна 0010111). На основе таких последовательностей построен, в частности, циклический избыточный код CRC32 (EDB88320).

Примечания

1. ↑ Встречаются также написания «де Бройна» и «де Брюина».
2. ↑ N. G. de Bruijn, A combinatorial problem // Koninklijke Nederlandse Akademie v. Wetenschappen, v. 49, 1946, pp. 758—764.
3. ↑ C. Flye Sainte-Marie, Question 48 // L'intermédiaire math., v. 1, 1894, pp. 107—110.