Формальное исчисление

Форма́льная (аксиоматическая) тео́рия, формальное исчисление — это понятие, разработанное в рамках формальной логики в качестве основы для формализации теории доказательства. Формальная теория — разновидность дедуктивной теории, где множество теорем выделяется из множества формул путем задания множества аксиом и правил вывода.

Определение

Формальная теория 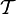$\mathcal{T}$ — это:

1. конечное множество 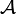$\mathcal{A}$ символов, образующих алфавит;
2. конечное множество 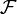$\mathcal{F}$ слов в алфавите 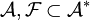$\mathcal{A}, \mathcal{F}\sub \mathcal{A}^*$, которые называются формулами;
3. подмножество 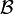$\mathcal{B}$ формул, 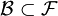$\mathcal{B}\sub \mathcal{F}$, которые называются аксиомами;
4. множество 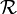$\mathcal{R}$ отношений 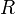$R\,\!$ на множестве формул, 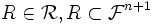$R \in \mathcal{R}, R \sub \mathcal{F}^{n+1}$, которые называются правилами вывода.

Множество символов 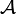$\mathcal{A}$ может быть конечным или бесконечным. Обычно для образования символов используют конечное множество букв, к которым при необходимости приписываются в качестве индексов целые числа или выражения.

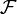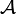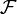Множество формул $\mathcal{F}$ обычно задаётся индуктивным определением, например, с помощью формальной грамматики. Как правило, это множество бесконечно. Множества $\mathcal{A}$ и $\mathcal{F}$ в совокупности определяют язык или сигнатуру формальной теории.

Множество аксиом 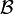$\mathcal{B}$ может быть конечным или бесконечным. Если множество аксиом бесконечно, то, как правило, оно задаётся с помощью конечного числа схем аксиом и правил порождения конкретных аксиом из схемы аксиом. Обычно аксиомы делятся на два вида: логические аксиомы (общие для целого класса формальных теорий) и нелогические или собственные аксиомы (определяющие специфику и содержание конкретной теории).

Множество правил вывода 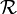$\mathcal{R}$, как правило, конечно.

См. также

• Дедуктивная теория

Литература

• Ф. А. Новиков. Дискретная математика для программистов. — СПб.: Питер, 2000. — 304 с.: ил. ISBN 5-272-00183-4.