- ВЫВОД ()
- ВЫВОД (в математической логике)
-
В. обычно называется рассуждение, в ходе к-рого последовательно получается ряд связанных друг с другом предложений, а также и сама последовательность этих предложений. Нек-рые из числа этих предложений не обосновываются в пределах данного В. и называются либо аксиомами, если их истинность принимается нами без доказательства, либо же посылками или гипотезами этого В., а истинность каждого из остальных предложений вытекает из истинности каких-то ранее сформулированных в данном В. предложений (часто В. также наз. не само рассуждение, а лишь его заключит. результат – последнее предложение в цепи связанных между собой предложений).Практика человеч. мышления показывает, что, обосновывая истинность нек-рого предложения А истинностью каких-то предложений В1,...,Вn, мы иногда пользуемся такими закономерностями, к-рые имеют настолько общий характер, что верны при любом содержании как предложений В1,...,Вn, так и предложения А, т.е. независимо от этого содержания, и зависят только от того, что принято называть логич. формой или структурой предложений В1,...,Вn, А. Такие закономерности носят название логических, а их формулировки называются логич. правилами. Если при обосновании предложений нек-рого В. используется только логич. закономерность, то такой В. носит название формального или логич. В.В зависимости от того, насколько подробно излагается тот или иной формальный В., он может быть либо более лаконичным, сводясь исключительно, или почти исключительно к одним только логически следующим друг "а друга предложениям, либо же, напротив, он может быть более или менее детальным и сопровождать появление нек-рых, или даже каждого нового предложения, точным указанием того, из каких именно предыдущих предложений получается это новое предложение. Т.о., всякий формальный В. состоит из последовательности предложений, логически связанных друг с другом, и может, кроме того, содержать т.н. анализ, в к-ром для нек-рых или для каждого предложения последовательности указывается, является ли оно гипотезой данного В. или аксиомой, а если нет, то из каких именно предыдущих предложений оно следует. Одним из возможных способов задания анализа нек-рого В. является расположение его предложений в виде "дерева". Пусть, напр., у нас имеется В., состоящий из пяти предложений Α1, Α2, А3, А4 и А5, из к-рых Α1, Α2, А3 являются гипотезами данного вывода, А4, получается (следует) из Α1 и Α2, а А5 получается из А4 и гипотезы А3. Тогда мы можем описать этот же анализ, следующим образом располагая предложения Α1, Α2, А3,А4,А5:
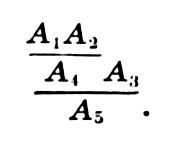 С понятием формального В. тесно связано понятие выводимости. Предложение А называется выводимым из гипотез Г1, Г2,...,Гn, если существует хотя бы один формальный В., последним предложением к-рого было бы предложение А и гипотезами к-рого были бы предложения Г1,...,Гn Этим понятием определяется нек-рое отношение – отношение выводимости, в к-ром могут находиться, с одной стороны, совокупности предложений Г1,...,Гn (в качестве посылок), а с другой – отд. предложения А (в качестве заключений).Хотя формальные В., используемые математикой, ничем принципиально не отличаются от формальных В. вообще, тем не менее специфика изучаемого математикой содержания привела к тому, что именно в математике формальные В. получили наибольшее распространение и в настоящее время являются одной из легче всего замечаемых отличит. черт математики как науки.Математика не только использует формальный В. как инструмент, но и занимается исследованием проблем, связанных с использованием этого инструмента познания. При этом ставится задача создания, а также и исследования свойств и границ возможного применения различных формальных аппаратов, к-рые позволяли бы чисто формально, без учета содержания, преобразовывать предложения и к-рые при этом всегда давали бы в качестве результата истинные предложения, если только посылки были истинными. Теорией формального В. занимается математич. логика.Делая формальный вывод объектом математич. исследования, математич. логика преобразует это понятие следующим образом. Прежде всего уточняется используемое в нем понятие логич. следования. Это достигается явным указанием тех правил В., к-рые разрешается использовать для получения новых предложений из ранее полученных. Теперь в анализе нек-рого конкретного В. по отношению к каждому предложению, не являющемуся гипотезой или аксиомой этого В., должно быть указано не только то, из каких предыдущих предложений оно получается, но и по какому правилу В. Примером правила В. может служить, скажем, следующее: из предложения "Если А, то В" и предложения "А" следует (или выводится) предложение "В", где А и В могут быть предложениями произвольного вида. В общем случае всякое правило В. является утверждением типа:"Из предложений А1,...,Аn, имеющих каждое такой-то вид, следует (или выводится) предложение В такого-то вида". В этом случае А1,...,Аn называются посылками данного правила, а В – его заключением.Самым существенным здесь является то, что в правилах В. указывается лишь вид посылок и заключения – их структура – и никогда не упоминается их содержание. Вследствие этого, решая вопрос о том, следует ли нек-рое конкретное предложение В из нек-рых конкретных предложений А1,..., Аn по какому-то определ. правилу В., мы никак не можем использовать содержание этих предложений, то есть вынуждены обращаться с ними как с последовательностями символов, как с материальными объектами определенной структуры и не более того. Поэтому мы можем смотреть на формальный В. как на последовательность материальных объектов, игнорируя тот факт, что эти объекты являются предложениями, имеющими какое-то содержание. Этим, в частности, объясняется то, что пока занимаются теорией формального В., бесполезно строить предложения из отд. слов, из к-рых каждое в свою очередь составляется из целого ряда букв. Вместо этого появляется возможность ввести спец. символику, в к-рой слова или даже целые предложения обозначаются одним или несколькими символами. От этой символики требуется, чтобы с ее помощью можно было хорошо передавать логич. структуру предложений и совершенно безразлично, можно ли с ее помощью передавать их содержание, к-рое все равно не может быть использовано в формальном В. Так, напр., предложение "Если А, то В" удобнее записывать в виде "А ⊃ В"; предложение, отрицающее то, что утверждается в предложении А, удобнее записывать в виде "ВЫВОД (в математической логике) А", и т.д.Математич. логика изучает формальный В. в рамках т.н. формальных систем, примеры к-рых рассмотрены ниже (др. употребит. названия – логистич. система, логич. исчисление формальное исчисление, логич. формализм и т.д.).Изучая различные формальные исчисления и используя формализованные в них понятия В. и выводимости, математич. логика решает такие проблемы, к-рые иными средствами невозможно было бы не только решить, но даже точно поставить. Это, разумеется, не значит, что нельзя пользоваться неформализованными понятиями В. и выводимости. Но доказывать с математич. строгостью теоремы об этих понятиях можно лишь в том случае, если смотреть на В. как на материальный объект. Значение полученных таким путем результатов целиком определяется тем, насколько полно и верно нам удалось отобразить свойства В. и выводимости при их формализации. Разработка т. зр., согласно к-рой формальные логич. операции совершаются над символами и последовательностями символов, т.е. над материальными объектами, позволила широко поставить проблему алгоритмизации логич. процессов (см. Алгоритм) и подготовить передачу машинам выполнение нек-рых логич. операций. Действительно, схема использования машины для решения логич. задач такова: нек-рая исходная информация, заданная в виде осмысленных предложений, кодируется, т.е. переводится на спец. язык, и передается машине; машина преобразует эти предложения, оперируя с ними как с материальными объектами, лишенными содержания; результат этих преобразований вновь истолковывается как предложения на нек-ром спец. языке, т е. как нечто осмысленное, и затем раскодируется, принимая привычную нам речевую форму. Среднее звено этого процесса как раз и есть практич. воплощение той т. зр., на к-рой стоит математич. логика, когда она рассматривает предложения как лишенные содержания наборы символов, а В. – как последовательности таких наборов.В качестве примера формальной системы рассмотрим одно из возможных построений т.н. исчисления высказываний, или, как его также иногда называют, "пропозиционального исчисления". Вначале зададим исходные символы, с помощью к-рых будут строиться все выражения системы (как говорят, зададим алфавит системы). Пусть ими будут: во-первых, бесконечный перечень символов: p q r s p1 q1 r1 s1 p2 q2... и т.д. (эти символы будем называть пропозициональными переменными), и, во-вторых, четыре символа[ ] ⊃ ВЫВОД (в математической логике)(из к-рых два первых являются левой и правой скобками, а два последних называются соответственно знаками импликации и отрицания). Затем укажем правила, по к-рым из исходных символов можно будет последовательно строить все более сложные выражения данной системы, к-рые будут называться "формулами". Этими правилами построения являются следующие:1) Всякая пропозициональная переменная есть формула.2) Если А и В суть формулы, то [А⊃В] есть формула.3) Если А есть формула, то ВЫВОД (в математической логике) А есть формула. Следующие три формулы будем называть "аксиомами" нашей системы:
С понятием формального В. тесно связано понятие выводимости. Предложение А называется выводимым из гипотез Г1, Г2,...,Гn, если существует хотя бы один формальный В., последним предложением к-рого было бы предложение А и гипотезами к-рого были бы предложения Г1,...,Гn Этим понятием определяется нек-рое отношение – отношение выводимости, в к-ром могут находиться, с одной стороны, совокупности предложений Г1,...,Гn (в качестве посылок), а с другой – отд. предложения А (в качестве заключений).Хотя формальные В., используемые математикой, ничем принципиально не отличаются от формальных В. вообще, тем не менее специфика изучаемого математикой содержания привела к тому, что именно в математике формальные В. получили наибольшее распространение и в настоящее время являются одной из легче всего замечаемых отличит. черт математики как науки.Математика не только использует формальный В. как инструмент, но и занимается исследованием проблем, связанных с использованием этого инструмента познания. При этом ставится задача создания, а также и исследования свойств и границ возможного применения различных формальных аппаратов, к-рые позволяли бы чисто формально, без учета содержания, преобразовывать предложения и к-рые при этом всегда давали бы в качестве результата истинные предложения, если только посылки были истинными. Теорией формального В. занимается математич. логика.Делая формальный вывод объектом математич. исследования, математич. логика преобразует это понятие следующим образом. Прежде всего уточняется используемое в нем понятие логич. следования. Это достигается явным указанием тех правил В., к-рые разрешается использовать для получения новых предложений из ранее полученных. Теперь в анализе нек-рого конкретного В. по отношению к каждому предложению, не являющемуся гипотезой или аксиомой этого В., должно быть указано не только то, из каких предыдущих предложений оно получается, но и по какому правилу В. Примером правила В. может служить, скажем, следующее: из предложения "Если А, то В" и предложения "А" следует (или выводится) предложение "В", где А и В могут быть предложениями произвольного вида. В общем случае всякое правило В. является утверждением типа:"Из предложений А1,...,Аn, имеющих каждое такой-то вид, следует (или выводится) предложение В такого-то вида". В этом случае А1,...,Аn называются посылками данного правила, а В – его заключением.Самым существенным здесь является то, что в правилах В. указывается лишь вид посылок и заключения – их структура – и никогда не упоминается их содержание. Вследствие этого, решая вопрос о том, следует ли нек-рое конкретное предложение В из нек-рых конкретных предложений А1,..., Аn по какому-то определ. правилу В., мы никак не можем использовать содержание этих предложений, то есть вынуждены обращаться с ними как с последовательностями символов, как с материальными объектами определенной структуры и не более того. Поэтому мы можем смотреть на формальный В. как на последовательность материальных объектов, игнорируя тот факт, что эти объекты являются предложениями, имеющими какое-то содержание. Этим, в частности, объясняется то, что пока занимаются теорией формального В., бесполезно строить предложения из отд. слов, из к-рых каждое в свою очередь составляется из целого ряда букв. Вместо этого появляется возможность ввести спец. символику, в к-рой слова или даже целые предложения обозначаются одним или несколькими символами. От этой символики требуется, чтобы с ее помощью можно было хорошо передавать логич. структуру предложений и совершенно безразлично, можно ли с ее помощью передавать их содержание, к-рое все равно не может быть использовано в формальном В. Так, напр., предложение "Если А, то В" удобнее записывать в виде "А ⊃ В"; предложение, отрицающее то, что утверждается в предложении А, удобнее записывать в виде "ВЫВОД (в математической логике) А", и т.д.Математич. логика изучает формальный В. в рамках т.н. формальных систем, примеры к-рых рассмотрены ниже (др. употребит. названия – логистич. система, логич. исчисление формальное исчисление, логич. формализм и т.д.).Изучая различные формальные исчисления и используя формализованные в них понятия В. и выводимости, математич. логика решает такие проблемы, к-рые иными средствами невозможно было бы не только решить, но даже точно поставить. Это, разумеется, не значит, что нельзя пользоваться неформализованными понятиями В. и выводимости. Но доказывать с математич. строгостью теоремы об этих понятиях можно лишь в том случае, если смотреть на В. как на материальный объект. Значение полученных таким путем результатов целиком определяется тем, насколько полно и верно нам удалось отобразить свойства В. и выводимости при их формализации. Разработка т. зр., согласно к-рой формальные логич. операции совершаются над символами и последовательностями символов, т.е. над материальными объектами, позволила широко поставить проблему алгоритмизации логич. процессов (см. Алгоритм) и подготовить передачу машинам выполнение нек-рых логич. операций. Действительно, схема использования машины для решения логич. задач такова: нек-рая исходная информация, заданная в виде осмысленных предложений, кодируется, т.е. переводится на спец. язык, и передается машине; машина преобразует эти предложения, оперируя с ними как с материальными объектами, лишенными содержания; результат этих преобразований вновь истолковывается как предложения на нек-ром спец. языке, т е. как нечто осмысленное, и затем раскодируется, принимая привычную нам речевую форму. Среднее звено этого процесса как раз и есть практич. воплощение той т. зр., на к-рой стоит математич. логика, когда она рассматривает предложения как лишенные содержания наборы символов, а В. – как последовательности таких наборов.В качестве примера формальной системы рассмотрим одно из возможных построений т.н. исчисления высказываний, или, как его также иногда называют, "пропозиционального исчисления". Вначале зададим исходные символы, с помощью к-рых будут строиться все выражения системы (как говорят, зададим алфавит системы). Пусть ими будут: во-первых, бесконечный перечень символов: p q r s p1 q1 r1 s1 p2 q2... и т.д. (эти символы будем называть пропозициональными переменными), и, во-вторых, четыре символа[ ] ⊃ ВЫВОД (в математической логике)(из к-рых два первых являются левой и правой скобками, а два последних называются соответственно знаками импликации и отрицания). Затем укажем правила, по к-рым из исходных символов можно будет последовательно строить все более сложные выражения данной системы, к-рые будут называться "формулами". Этими правилами построения являются следующие:1) Всякая пропозициональная переменная есть формула.2) Если А и В суть формулы, то [А⊃В] есть формула.3) Если А есть формула, то ВЫВОД (в математической логике) А есть формула. Следующие три формулы будем называть "аксиомами" нашей системы: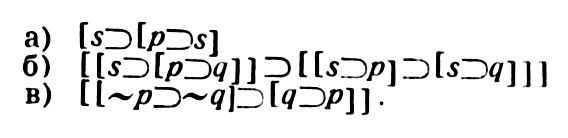 Наконец, возьмем в качестве правил В. следующие два правила:I) Если формула А' получается из формулы А путем замены нек-рой пропозициональной переменной (всюду, где она встречается в А) на формулу С, то из А следует А' (правило подстановки).II) Из формул вида [А⊃В] и формулы А следует формула В (правило модус поненс).Такое задание формальной системы, когда указывается ее алфавит, правила построения, правила В. и "аксиомы", является довольно типичным, хотя и не единственно возможным.Следует иметь в виду, что в данном случае с термином "аксиома не связывается ничего, что соответствовало бы обычному представлению об аксиомах как о предложениях, истинность к-рых принимается без доказательства. В данном случае это просто формулы, выделенные из общей массы формул формальной системы и играющие особую роль при определении понятий "доказательство" и "теорема" (см. ниже).Задавая нек-рую формальную систему, используют какую-то часть содержательного разговорного языка, к-рая по отношению к задаваемой формальной системе называется метаязыком. Этот метаязык используется как при построении формальной системы, так и для того, чтобы высказать утверждения о формальной системе. Так, напр., предложениями метаязыка являются правила В. и правила построения, а такие встречающиеся в них обозначения, как, напр., [А⊃В], являются элементами не формальной системы, а ее метаязыка. Этот метаязык может оставаться неформализованным, как в рассматриваемом случае, но может быть и формализован и превращен в нек-рую формальную систему (метасистему по отношению к первой системе). Для этого в свою очередь потребовался бы нек-рый содержат. мета-метаязык и т.д. Определим теперь для этой системы понятия В. и выводимости: Последовательность формул А1,...,Аn называется В. формулы А из гипотез Г1,...,Гm, если формула А есть последняя формула последовательности А1,...,Аn и если каждая формула этой последовательности есть либо аксиома системы, либо одна из гипотез Г1,..., либо получается из каких-то предыдущих формул и последовательности по одному из правил В. системы.В. из пустого множества гипотез называется доказательством.Формула А, для к-рой существует хотя бы один В. из гипотез Г1,..., Гm, называется выводимой из Г1, Гт. Утверждение о выводимости А из гипотез Г1,..., Гт часто обозначают так: Г1,..., Гm, |– А. Т.о., знак "|–" является сокращением, используемым в содержат. метаязыке. Формула А, для к-рой существует доказательство (т.е. В. из пустого множества гипотез), называется доказуемой формулой или теоремой формальной системы (обозначение: |– А).В соответствии с привед. определениями последовательность из трех формул [p⊃q], r [[p⊃q]⊃ r], r является В. формулы r из гипотез [p⊃q] и [[p⊃q]⊃r] по правилу модус поненс. Т.о.,
Наконец, возьмем в качестве правил В. следующие два правила:I) Если формула А' получается из формулы А путем замены нек-рой пропозициональной переменной (всюду, где она встречается в А) на формулу С, то из А следует А' (правило подстановки).II) Из формул вида [А⊃В] и формулы А следует формула В (правило модус поненс).Такое задание формальной системы, когда указывается ее алфавит, правила построения, правила В. и "аксиомы", является довольно типичным, хотя и не единственно возможным.Следует иметь в виду, что в данном случае с термином "аксиома не связывается ничего, что соответствовало бы обычному представлению об аксиомах как о предложениях, истинность к-рых принимается без доказательства. В данном случае это просто формулы, выделенные из общей массы формул формальной системы и играющие особую роль при определении понятий "доказательство" и "теорема" (см. ниже).Задавая нек-рую формальную систему, используют какую-то часть содержательного разговорного языка, к-рая по отношению к задаваемой формальной системе называется метаязыком. Этот метаязык используется как при построении формальной системы, так и для того, чтобы высказать утверждения о формальной системе. Так, напр., предложениями метаязыка являются правила В. и правила построения, а такие встречающиеся в них обозначения, как, напр., [А⊃В], являются элементами не формальной системы, а ее метаязыка. Этот метаязык может оставаться неформализованным, как в рассматриваемом случае, но может быть и формализован и превращен в нек-рую формальную систему (метасистему по отношению к первой системе). Для этого в свою очередь потребовался бы нек-рый содержат. мета-метаязык и т.д. Определим теперь для этой системы понятия В. и выводимости: Последовательность формул А1,...,Аn называется В. формулы А из гипотез Г1,...,Гm, если формула А есть последняя формула последовательности А1,...,Аn и если каждая формула этой последовательности есть либо аксиома системы, либо одна из гипотез Г1,..., либо получается из каких-то предыдущих формул и последовательности по одному из правил В. системы.В. из пустого множества гипотез называется доказательством.Формула А, для к-рой существует хотя бы один В. из гипотез Г1,..., Гm, называется выводимой из Г1, Гт. Утверждение о выводимости А из гипотез Г1,..., Гт часто обозначают так: Г1,..., Гm, |– А. Т.о., знак "|–" является сокращением, используемым в содержат. метаязыке. Формула А, для к-рой существует доказательство (т.е. В. из пустого множества гипотез), называется доказуемой формулой или теоремой формальной системы (обозначение: |– А).В соответствии с привед. определениями последовательность из трех формул [p⊃q], r [[p⊃q]⊃ r], r является В. формулы r из гипотез [p⊃q] и [[p⊃q]⊃r] по правилу модус поненс. Т.о.,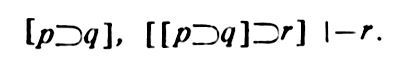
 Т.о., |– [s⊃s] т.е. формула эта доказуема в формальной системе, или, что то же самое, является в ней теоремой. Иногда в качестве выводов формальной системы вместо вышеописанных последовательностей рассматривают какой-либо более ограниченный класс последовательностей. Обычно это мотивируется желанием формулировать без всяких ограничений т.н. дедукционную теорему ("Если Г1, Г2,..., Гn, А |– В, то Г1, Г2,..., Гn |– А⊃"). Эта теорема, являющаяся, разумеется, не "теоремой" формального исчисления, а содержат. теоремой метаязыка, имеет очень большое эвристич. значение, т.к. позволяет использовать в процессе выведения вспомогат. допущения, исключаемые затем с ее помощью из числа гипотез (подробнее см. ниже). В рассматриваемом случае желаемого результата можно добиться, потребовав, напр., в определении В., чтобы в тех случаях, когда подстановки в соответствии с правилами вывода 1) совершаются в формулы, не являющиеся аксиомами, они не совершались бы вместо переменных, входящих в к.-л. гипотезу. Примем это ограничение.Если различным образом менять определение В., то тем самым будет меняться и отношение выводимости в формальной системе. Это, однако, не должно вести к изменению понятия доказуемости (выводимости из пустого множества гипотез), т.е. множество теорем системы должно при этом оставаться неизменным, т.к. иначе мы получили бы уже другую формальную систему.Отношение выводимости "|–", к-рое мы определили в метаязыке через понятие В. рассматриваемой формальной системы, обладает целым рядом свойств, к-рые приводятся ниже. Формулировки свойств даны в сокращенной записи, в к-рой X и Y понимаются как произвольные формулы формальной системы, а G и H суть произвольные (в частности, может быть, и пустые) списки формул:(1) Х |– X(2) ВЫВОД (в математической логике) ВЫВОД (в математической логике)Х |– X(3) Если совокупность Н отличается от совокупности G только порядком входящих в нее формул, то: если G |– X, то и H |– X
Т.о., |– [s⊃s] т.е. формула эта доказуема в формальной системе, или, что то же самое, является в ней теоремой. Иногда в качестве выводов формальной системы вместо вышеописанных последовательностей рассматривают какой-либо более ограниченный класс последовательностей. Обычно это мотивируется желанием формулировать без всяких ограничений т.н. дедукционную теорему ("Если Г1, Г2,..., Гn, А |– В, то Г1, Г2,..., Гn |– А⊃"). Эта теорема, являющаяся, разумеется, не "теоремой" формального исчисления, а содержат. теоремой метаязыка, имеет очень большое эвристич. значение, т.к. позволяет использовать в процессе выведения вспомогат. допущения, исключаемые затем с ее помощью из числа гипотез (подробнее см. ниже). В рассматриваемом случае желаемого результата можно добиться, потребовав, напр., в определении В., чтобы в тех случаях, когда подстановки в соответствии с правилами вывода 1) совершаются в формулы, не являющиеся аксиомами, они не совершались бы вместо переменных, входящих в к.-л. гипотезу. Примем это ограничение.Если различным образом менять определение В., то тем самым будет меняться и отношение выводимости в формальной системе. Это, однако, не должно вести к изменению понятия доказуемости (выводимости из пустого множества гипотез), т.е. множество теорем системы должно при этом оставаться неизменным, т.к. иначе мы получили бы уже другую формальную систему.Отношение выводимости "|–", к-рое мы определили в метаязыке через понятие В. рассматриваемой формальной системы, обладает целым рядом свойств, к-рые приводятся ниже. Формулировки свойств даны в сокращенной записи, в к-рой X и Y понимаются как произвольные формулы формальной системы, а G и H суть произвольные (в частности, может быть, и пустые) списки формул:(1) Х |– X(2) ВЫВОД (в математической логике) ВЫВОД (в математической логике)Х |– X(3) Если совокупность Н отличается от совокупности G только порядком входящих в нее формул, то: если G |– X, то и H |– X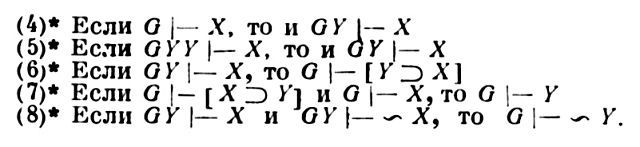 Утверждения (1) – (8) являются сокращенно записанными содержат. предложениями метаязыка и могут быть доказаны как математич. теоремы. Два из них, а именно (1) и (2), утверждают, что в данной системе существуют выводы определенного вида, а остальные дают достаточные условия существования некоторых выводов. В этих предложениях фигурирует понятие "выводимо", к-рое было введено для этой формальной системы и к-рое, разумеется, отлично от соответств. понятия содержат. логики человеч. мышления. Если, однако, считать формулы вида [А⊃В] сокращениями вместо обычных условных предложений "Если А, то В" и формулы вида ВЫВОД (в математической логике) А – обычными отрицаниями вида "не-A" и переистолковать утверждения (1) – (8) как утверждения об обычных предложениях и обычной выводимости, то все они окажутся естественными. Это может служить иллюстрацией того, в каком смысле построенный аппарат пропозицион. исчисления может считаться своего рода приближением к нек-рой части логики человеч. мышления.Связь между построенным нами пропозицион. исчислением и содержат. мышлением можно проиллюстрировать еще и на таком примере. В обычных содержат. рассуждениях часто используется прием, заключающийся во введении в В. тех или иных вспомогат. допущений. Следствия из этих допущений так или иначе используются в В., но сами допущения впоследствии исключаются, так что окончат., результат оказывается от них не зависящим. Примером рассуждения такого типа может служить всякое доказательство "от противного". Схема рассуждения "от противного" такова: Пусть нам требуется вывести предложение А от гипотез Г1, Г2,...,Гn. Вводим (временное) вспомогат. допущение не-А (противное тому, что требуется доказать) и затем тем или иным путем выводим из совокупности гипотез Г1, Г2,...,Гn, не-А следствие не-Гn. Так как из той же совокупности гипотез можно вывести и следствие Гn, то заключаем, что предположение не-А противоречит совокупности гипотез Г1, Г2,...,Гn: следовательно, из гипотез Г1, Г2, Гn следует А. Существенно, что, формулируя окончат. результат, можно не причислять временное допущение не-А к числу гипотез; заключение А зависит от гипотез Г1, Г2,...,Гn, но не зависит от не-А.Оказывается, что метод вспомогат. допущений находит отражение в пропозицион. исчислении, причем путь к этому открывается уже упоминавшейся дедукционной теоремой. Напр., доказательство "от противного" выглядит в пропозицион. исчислении след. образом. Требуется вывести предложение А из гипотез Г1, Г2,..., Гn, т.е. доказать, что Г1, Г2,..., Гn |– А. Присоединяем к гипотезам временное допущение ВЫВОД (в математической логике) А и доказываем, что Г1, Г2,..., Гn ВЫВОД (в математической логике) Α |– ВЫВОД (в математической логике) Гп. Затем по дедукционной теореме заключаем, что Г1, Г2,..., Гn |– ВЫВОД (в математической логике) A ⊃ ВЫВОД (в математической логике) Гn, исключая, т.о., временное допущение ВЫВОД (в математической логике) А из числа гипотез. Дальше можно вести доказательство совершенно параллельно вышеописанному содержат, рассуждению и свести дело к непосредств. использованию закона противоречия, но сейчас удобнее продолжить его иначе. В пропозицион. исчислении имеется аксиома [[ ВЫВОД (в математической логике) p ⊃ ВЫВОД (в математической логике) q] ⊃ [q ⊃ p ]]. Подставляя А вместо р и Гn вместо q, получаем из нее, что |– [[ ВЫВОД (в математической логике) Α ⊃ ВЫВОД (в математической логике) Гn ] ⊃ Х Х [ Гn ⊃ Α ]]. Тогда n раз применяя свойство выводимости (4)* (при пустом G, получаем постепенно, что Г1, Г2,..., Гn |– [[ ВЫВОД (в математической логике) A ⊃ Гn] ⊃ [ Гn ⊃ A ]]. Далее, по свойству (7)* получаем, что Г1, Г2,..., Гn |– Гn ⊃ A, так как по (1)* имеет место Гn |– Гn и, следовательно, по (4)* – Г1, Г2,..., Гn |– Гn, то, еще раз применяя (7)*, получаем окончательно Г1, Г2,..., Гn |– А.Хотя введенное для пропозицион. исчисления понятие выводимости и отличается от понятия выводимости в обычном содержат. мышлении, оно все же есть понятие содержательное – в том смысле, что утверждение о выводимости нек-рой формулы из нек-рых гипотез есть утверждение о существовании материального объекта (последовательности формул) с определ. свойствами. В соответствии с этим знак |– является содержат. сокращением, а, напр., запись X ВЫВОД (в математической логике) X |– Y содержат. утверждением, к-рое можно расшифровать так: "Если в качестве гипотез взять любую формулу X и ее формальное отрицание ВЫВОД (в математической логике) X, то для всякой формулы существует В. формулы Y из гипотез X и ВЫВОД (в математической логике) X. Возможен, однако, и другой подход к изучению выводимости. Можно построить другую формальную систему, к-рая давала бы возможность формально получать свойства выводимости в первой системе. Это можно сделать, напр., так.Возьмем за основу уже построенное нами пропозицион. исчисление и несколько видоизменим его. Прежде всего добавим к алфавиту системы новую букву "|–", к-рую не будем относить к числу пропозицион. переменных. Добавим далее к п р а в и л а м п о с т р о е н и я новое правило:4) Если G – произвольная совокупность формул (в частности – может быть и пустая) и А – произвольная формула, то G |– А есть предложение. Т.о., в новой формальной системе рассматриваются два вида выражений – "формулы" и "предложения", к-рые различаются тем, что в "предложениях" есть один знак "|–", а в "формулах" – нет. Содержательные сокращенные записи, напр. ранее доказанное для пропозицион. исчисления утверждение [ p ⊃ q ] [[ p ⊃ q ] ⊃ r ] |– r, превращаются в новой формальной системе в простые последовательности символов, а содержат. сокращение "|–" – в бессодержат. символ. В качестве системы аксиом новой системы возьмем бесконечное множество предложений вида (1)* и (2)*, т.е. все предложения, к-рые могут быть получены из (1)* и (2)*, если вместо X и Y подставлять всевозможные формулы.Наконец, в качестве правил В. новой системы возьмем (3)* – (8)*, предварительно заменив всюду оборот "Если..., то"..., на оборот "Из... следует...".Построив новую формальную систему, можно тем самым частично формализовать метаязык ранее построенной системы, о возможности чего уже говорилось. А именно, формализовано понятие выводимости, относящееся к прежней системе. Для новой системы можно определить относящиеся к ней понятия В. и выводимости так же, как это раньше было сделано для пропозицион. исчисления, причем новое отношение выводимости не имеет ничего общего со знаком "|–", к-рый является теперь бессодержат. символом системы.В новой системе является, напр., доказательством следующая последовательность "предложений":
Утверждения (1) – (8) являются сокращенно записанными содержат. предложениями метаязыка и могут быть доказаны как математич. теоремы. Два из них, а именно (1) и (2), утверждают, что в данной системе существуют выводы определенного вида, а остальные дают достаточные условия существования некоторых выводов. В этих предложениях фигурирует понятие "выводимо", к-рое было введено для этой формальной системы и к-рое, разумеется, отлично от соответств. понятия содержат. логики человеч. мышления. Если, однако, считать формулы вида [А⊃В] сокращениями вместо обычных условных предложений "Если А, то В" и формулы вида ВЫВОД (в математической логике) А – обычными отрицаниями вида "не-A" и переистолковать утверждения (1) – (8) как утверждения об обычных предложениях и обычной выводимости, то все они окажутся естественными. Это может служить иллюстрацией того, в каком смысле построенный аппарат пропозицион. исчисления может считаться своего рода приближением к нек-рой части логики человеч. мышления.Связь между построенным нами пропозицион. исчислением и содержат. мышлением можно проиллюстрировать еще и на таком примере. В обычных содержат. рассуждениях часто используется прием, заключающийся во введении в В. тех или иных вспомогат. допущений. Следствия из этих допущений так или иначе используются в В., но сами допущения впоследствии исключаются, так что окончат., результат оказывается от них не зависящим. Примером рассуждения такого типа может служить всякое доказательство "от противного". Схема рассуждения "от противного" такова: Пусть нам требуется вывести предложение А от гипотез Г1, Г2,...,Гn. Вводим (временное) вспомогат. допущение не-А (противное тому, что требуется доказать) и затем тем или иным путем выводим из совокупности гипотез Г1, Г2,...,Гn, не-А следствие не-Гn. Так как из той же совокупности гипотез можно вывести и следствие Гn, то заключаем, что предположение не-А противоречит совокупности гипотез Г1, Г2,...,Гn: следовательно, из гипотез Г1, Г2, Гn следует А. Существенно, что, формулируя окончат. результат, можно не причислять временное допущение не-А к числу гипотез; заключение А зависит от гипотез Г1, Г2,...,Гn, но не зависит от не-А.Оказывается, что метод вспомогат. допущений находит отражение в пропозицион. исчислении, причем путь к этому открывается уже упоминавшейся дедукционной теоремой. Напр., доказательство "от противного" выглядит в пропозицион. исчислении след. образом. Требуется вывести предложение А из гипотез Г1, Г2,..., Гn, т.е. доказать, что Г1, Г2,..., Гn |– А. Присоединяем к гипотезам временное допущение ВЫВОД (в математической логике) А и доказываем, что Г1, Г2,..., Гn ВЫВОД (в математической логике) Α |– ВЫВОД (в математической логике) Гп. Затем по дедукционной теореме заключаем, что Г1, Г2,..., Гn |– ВЫВОД (в математической логике) A ⊃ ВЫВОД (в математической логике) Гn, исключая, т.о., временное допущение ВЫВОД (в математической логике) А из числа гипотез. Дальше можно вести доказательство совершенно параллельно вышеописанному содержат, рассуждению и свести дело к непосредств. использованию закона противоречия, но сейчас удобнее продолжить его иначе. В пропозицион. исчислении имеется аксиома [[ ВЫВОД (в математической логике) p ⊃ ВЫВОД (в математической логике) q] ⊃ [q ⊃ p ]]. Подставляя А вместо р и Гn вместо q, получаем из нее, что |– [[ ВЫВОД (в математической логике) Α ⊃ ВЫВОД (в математической логике) Гn ] ⊃ Х Х [ Гn ⊃ Α ]]. Тогда n раз применяя свойство выводимости (4)* (при пустом G, получаем постепенно, что Г1, Г2,..., Гn |– [[ ВЫВОД (в математической логике) A ⊃ Гn] ⊃ [ Гn ⊃ A ]]. Далее, по свойству (7)* получаем, что Г1, Г2,..., Гn |– Гn ⊃ A, так как по (1)* имеет место Гn |– Гn и, следовательно, по (4)* – Г1, Г2,..., Гn |– Гn, то, еще раз применяя (7)*, получаем окончательно Г1, Г2,..., Гn |– А.Хотя введенное для пропозицион. исчисления понятие выводимости и отличается от понятия выводимости в обычном содержат. мышлении, оно все же есть понятие содержательное – в том смысле, что утверждение о выводимости нек-рой формулы из нек-рых гипотез есть утверждение о существовании материального объекта (последовательности формул) с определ. свойствами. В соответствии с этим знак |– является содержат. сокращением, а, напр., запись X ВЫВОД (в математической логике) X |– Y содержат. утверждением, к-рое можно расшифровать так: "Если в качестве гипотез взять любую формулу X и ее формальное отрицание ВЫВОД (в математической логике) X, то для всякой формулы существует В. формулы Y из гипотез X и ВЫВОД (в математической логике) X. Возможен, однако, и другой подход к изучению выводимости. Можно построить другую формальную систему, к-рая давала бы возможность формально получать свойства выводимости в первой системе. Это можно сделать, напр., так.Возьмем за основу уже построенное нами пропозицион. исчисление и несколько видоизменим его. Прежде всего добавим к алфавиту системы новую букву "|–", к-рую не будем относить к числу пропозицион. переменных. Добавим далее к п р а в и л а м п о с т р о е н и я новое правило:4) Если G – произвольная совокупность формул (в частности – может быть и пустая) и А – произвольная формула, то G |– А есть предложение. Т.о., в новой формальной системе рассматриваются два вида выражений – "формулы" и "предложения", к-рые различаются тем, что в "предложениях" есть один знак "|–", а в "формулах" – нет. Содержательные сокращенные записи, напр. ранее доказанное для пропозицион. исчисления утверждение [ p ⊃ q ] [[ p ⊃ q ] ⊃ r ] |– r, превращаются в новой формальной системе в простые последовательности символов, а содержат. сокращение "|–" – в бессодержат. символ. В качестве системы аксиом новой системы возьмем бесконечное множество предложений вида (1)* и (2)*, т.е. все предложения, к-рые могут быть получены из (1)* и (2)*, если вместо X и Y подставлять всевозможные формулы.Наконец, в качестве правил В. новой системы возьмем (3)* – (8)*, предварительно заменив всюду оборот "Если..., то"..., на оборот "Из... следует...".Построив новую формальную систему, можно тем самым частично формализовать метаязык ранее построенной системы, о возможности чего уже говорилось. А именно, формализовано понятие выводимости, относящееся к прежней системе. Для новой системы можно определить относящиеся к ней понятия В. и выводимости так же, как это раньше было сделано для пропозицион. исчисления, причем новое отношение выводимости не имеет ничего общего со знаком "|–", к-рый является теперь бессодержат. символом системы.В новой системе является, напр., доказательством следующая последовательность "предложений":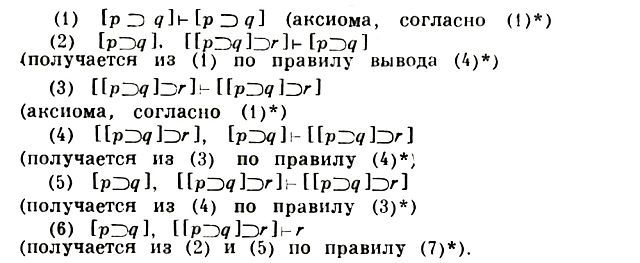 Т.о., доказано, что в новом исчислении предложение [p ⊃ q ], [[ p ⊃ q ] ⊃ ] |– r является теоремой. Для прежней системы было доказано нечто аналогичное, но в то время, как там это было содержат. утверждением, здесь это – бессодержат. набор символов.Однако новая система построена таким образом, что всякий раз, когда в прежнем исчислении доказуема нек-рая формула А, в новой системе доказуемо предложение – А, и наоборот, и каждый раз, когда в прежней системе формула А выводима из гипотез, в новой системе доказуемо предложение Г1,..., Гn |– А и наоборот. Это и дает возможность считать символ "|–" новой системы формализацией отношения выводимости прежней системы и использовать новую систему для изучения свойств выводимости в старой.Лит.: Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; Сhurсh Α., Introduction to mathematical logic, Princeton, 1956; Montague R. and Henkin L., On the definition of formal deduction, "J. Symbolic Logic", New Brunswick, 1956, v. 21, No 2, p. 129–36.В. Чернявский. Москва.
Т.о., доказано, что в новом исчислении предложение [p ⊃ q ], [[ p ⊃ q ] ⊃ ] |– r является теоремой. Для прежней системы было доказано нечто аналогичное, но в то время, как там это было содержат. утверждением, здесь это – бессодержат. набор символов.Однако новая система построена таким образом, что всякий раз, когда в прежнем исчислении доказуема нек-рая формула А, в новой системе доказуемо предложение – А, и наоборот, и каждый раз, когда в прежней системе формула А выводима из гипотез, в новой системе доказуемо предложение Г1,..., Гn |– А и наоборот. Это и дает возможность считать символ "|–" новой системы формализацией отношения выводимости прежней системы и использовать новую систему для изучения свойств выводимости в старой.Лит.: Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; Сhurсh Α., Introduction to mathematical logic, Princeton, 1956; Montague R. and Henkin L., On the definition of formal deduction, "J. Symbolic Logic", New Brunswick, 1956, v. 21, No 2, p. 129–36.В. Чернявский. Москва.
Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.
.
