Форда-Фалкерсона теорема

Теорема Форда — Фалкерсо́на — теорема о максимальном потоке в графе.

Звучит так: величина максимального потока равна величине минимального разреза.

Достаточность: любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть дан некоторый поток и некоторое сечение. Величина данного потока складывается из величин "грузов", перевозимых по всем возможным путям из вершины t в s. Каждый такой путь обязан иметь общее ребро с данным сечением. Так как по каждому ребру сечения суммарно нельзя перевести "груза" больше, чем его пропускная способность, поэтому сумма всех грузов меньше или равна сумме всех пропускных способностей рёбер данного сечения. Утверждение доказано.

Отсюда следует, что любой поток меньше или равен величине минимального сечения, а значит и максимальный поток меньше или равен величине минимального сечения.

На этой теореме основан алгоритм Форда — Фалкерсона поиска максимального потока в графе, он же является доказательством необходимости данной теоремы, т.е. оно явлвяется конструктивным.

Другое доказательство (через усиление)

Усилим теорему Форда-Фалкерсона следующим образом. Будем доказывать для сети G(V,E) с потоком f равносильность сразу трёх следующих фактов:

1° Поток f - максимальный

2° Пропускная способность минимального разреза равна величине потока f

3° В графе G нет дополняющего пути

1° → 3°. Предположив обратное, получим противоречие, описанное в информации по дополняющем пути в транспортном графе.

3° → 2°. Очевидно, что величина потока f не превышает пропускной способности минимального разреза (S,T). Пусть c(S,T) > f. Тогда рассмотрим разрез, где во множествеS будут все вершины, кроме t. Тогда его пропускная способность не меньше пропускной способности минимального разреза, что, в свою очередь, больше величины потока f. Значит, существует направление (u,t) из S в T, что f(u,t) < c(u,t). Теперь возьмём все такие u и перенесём их в T. Рассмотрев получившийся разрез, заметим, что его пропускная способность тоже меньше величины потока. Снова увеличиваем множество T и делаем так до тех пор, пока в множестве S не останется только вершина s. Она же будет первой вершиной в пути, который мы создаём. Теперь смотрим какую пару мы выбрали прошлым ходом. Пусть это пара (s,u). Тогда к пути добавляем вершину u. Далее смотрим в паре с какой вершиной была на первом месте вершина u. Пусть это (u,v). Тогда далее к пути добавляем вершину v. Делаем так до тех пор, пока не дойдём до вершины t. Однако по построению этот путь является остаточным, что противоречит предположению.

2° → 1°. Как уже говорилось, очевидно, что величина любого потока не превышает пропускной способности минимального разреза, а величина нашего потока f - равна. Тогда величина потока f не меньше величины любого другого потока в нашей сети, т.е. поток f - максимальный.

Это доказательство хорошо тем, что не использует сложный алгоритм нахождения максимального потока в произвольной транспортной сети.

Пример

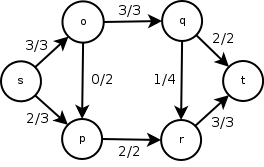Сеть с 3-мя минимальными разрезами

Справа дана сеть с 6-ю вершинами V = {s,o,p,q,r,t}, и суммарный поток от истока s к стоку t равен 5. Этот поток является максимальным для данной сети.

В данной сети возможны 3 минимальных разреза:

Cut	Capacity
S = {s,p},T = {o,q,r,t}	c(s,o) + c(p,r) = 3 + 2 = 5
S = {s,o,p},T = {q,r,t}	c(o,q) + c(p,r) = 3 + 2 = 5
S = {s,o,p,q,r},T = {t}	c(q,t) + c(r,t) = 2 + 3 = 5

Ссылки

• Алгоритм Форда-Фалкерсона на algolist.manual.ru.
• Сети, потоки в сетях. Теорема Форда – Фалкерсона на Mini-Soft.ru