Ультраметрика

В ультраметрическом пространстве у треугольника не бывает самой длинной стороны: либо равны все три, либо одна короче, а остальные две — равны

Ультраметрическое пространство — особый случай метрического пространства, в котором метрика удовлетворяет усиленному неравенству треугольника:

$d(x,z) \leqslant \max( d(x,y), d(y,z) )$

Такую метрику называют ультраметрикой. Проще говоря, в ультраметрическом пространстве нельзя получить большее расстояние, складывая меньшие.

Определение

Ультраметрическое пространство — это пара (M,d), где M — множество, а $d\colon M\times M \to \mathbb R$ — вещественнозначная функция на нём, также называемая метрикой, удовлетворяющая следующим условиям:

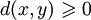1. $d(x,y) \geqslant 0$ (неотрицательность)
2. $d(x,y) = 0 \iff x=y$
3. d(x,y) = d(y,x) (симметричность)
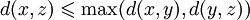4. $d(x,z) \leqslant \max( d(x,y), d(y,z) )$ (усиленное неравенство треугольника)

Ультраметрическое пространство отличается от метрического тем, что неравенство треугольника заменено на усиленное неравенство треугольника.

Свойства

• Всякий треугольник является равнобедренным, причём если не все его стороны равны, то одна — короче, чем две других.
• Всякая точка шара является его центром.
• Если два шара имеют общую точку, то либо они совпадают, либо один целиком содержит другой.
• Топология ультраметрического пространства является вполне разрывной.

Примеры

• Рассмотрим множество слов произвольной длины некоторого алфавита Σ. Положим d(a,b) = 2 ^{− n}, где n — номер первого символа, различного в словах a и b. Полученная функция будет ультраметрикой.
• Ультраметрика обычно связана со структурой направленного дерева.
• p-адические числа образуют ультраметрическое пространство с естественной ультраметрикой.
• Дискретная метрика (то есть расстояние между двумя точками равно 0 если они совпадают, и 1 если не совпадают) является ультраметрикой.
• Модели, наделённые естественной ультраметрикой, возникают в теории информации, при исследовании последовательностей символов, и физике твёрдого тела, при изучении спиновых стёкол.