тэта-функция — тэта/ функци/я [й/а] … Морфемно-орфографический словарь
Тэта-функции — целые функции (См. Целая функция), отношения которых представляют Эллиптические функции. Основные четыре Т. ф. определяются следующими быстро сходящимися рядами: θ1(z) = 2q 1/4sin z 2q 9/4 sin 3z + 2q 25/4 sin 5z +..., θ … Большая советская энциклопедия
θ-функция — Тэта функции специальные целые функции, отношения которых представляют эллиптические функции. Основные четыре Тэта функции определяются следующими быстро сходящимися рядами … Википедия
Θ-функция — Тэта функции специальные целые функции, отношения которых представляют эллиптические функции. Основные четыре Тэта функции определяются следующими быстро сходящимися рядами … Википедия
Эллиптические функции Якоби — Эллиптические функции Якоби это набор основных эллиптических функций комплексного переменного, и вспомогательных тэта функций, которые имеют прямое отношение к некоторым прикладным задачам (например, уравнение маятника). Они также имеют… … Википедия
Сигма-функции — целые Трансцендентные функции, введённые К. Вейерштрассом при построении им своей теории эллиптических функций. Основной из четырёх С. ф. является функция где ω = 2mω1 + 2nω2, ω1 и ω2 два числа, отношение которых не… … Большая советская энциклопедия
Фурье преобразование — (данной функции) функция, выражающаяся через данную функцию f (x) формулой: Если функция f (x) чётная, то её ф. п. равно (косинус преобразование), а если f (x) нечётная функция, то … … Большая советская энциклопедия
Список математических функций — Эта страница информационный список. В математике, многие функции и группы функций настолько важны, что заслужили право на собственные имена. Ниже приведён список статей, которые содержат подробные описания некоторых из таких функций … Википедия
Эллиптические функции — функции, связанные с обращением эллиптических интегралов (См. Эллиптические интегралы). Э. ф. применяются во многих разделах математики и механики как при теоретических исследованиях, так и для численных расчётов. Подобно тому… … Большая советская энциклопедия
МОДУЛЯРНАЯ ФОРМА — одного комплексного переменного, эллиптическая модулярная форм а, функция на верхней полуплоскости , удовлетворяющая при нек ром фиксированном кусловию автоморфности: для любого элемента группы целочисленных матриц с определителем , и такая, что… … Математическая энциклопедия



 где
где  .
. к аргументу
к аргументу  эти функции приобретают соответственно множители −1, −1, 1, 1, а при добавлении
эти функции приобретают соответственно множители −1, −1, 1, 1, а при добавлении  , где
, где 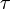 связано с
связано с  соотношением
соотношением  , множители
, множители  . Отсюда следует, что, например, отношение
. Отсюда следует, что, например, отношение  представляет мероморфную функцию, не изменяющуюся при добавлении к аргументу
представляет мероморфную функцию, не изменяющуюся при добавлении к аргументу  или
или  , то есть эллиптическую функцию с периодами
, то есть эллиптическую функцию с периодами  или
или  .
.