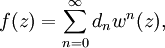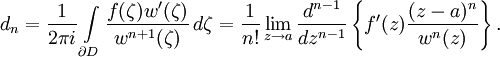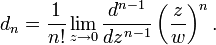Ряд Бурмана — Лагранжа

Ряд Бюрмана — Лагранжа определяется как разложение аналитической функции f(z) по степеням другой аналитической функции w(z) и представляет собой далеко идущее обобщение ряда Тейлора.

Пусть f(z) и w(z) аналитичны в окрестности некоторой точки 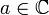$a\in\C$, притом w(a) = 0 и a — простой нуль функции w(z). Теперь выберем некую область 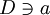$D\ni a$, в которой f и w аналитичны, а w однолистна в 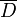$\overline{D}$. Тогда имеет место разложение вида:

$f(z)=\sum_{n=0}^\infty d_n w^n(z),$

где коэффициенты d_n вычисляются по следующему выражению:

$d_n=\frac{1}{2\pi i}\int\limits_{\partial D}\frac{f(\zeta)w'(\zeta)}{w^{n+1}(\zeta)}\,d\zeta=\frac{1}{n!}\lim_{z\to a}\frac{d^{n-1}}{dz^{n-1}}\left\{f'(z)\frac{(z-a)^n}{w^n(z)}\right\}.$

Теорема об обращении рядов

Частным случаем применения рядов является так называемая задача об обращении ряда Тейлора.

Рассмотрим разложение вида 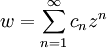$w=\sum_{n=1}^\infty c_nz^n$. Попытаемся с помощью полученного выражения вычислить коэффициенты ряда $z=\sum_{n=1}^\infty d_nw^n$:

$d_n=\frac{1}{n!}\lim_{z\to 0}\frac{d^{n-1}}{dz^{n-1}}\left(\frac{z}{w}\right)^n.$

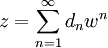Литература

• Шабат Б. В. Введение в комплексный анализ. — М.: Наука. — 1969, 577 стр.