- Репрезентативное подпространство
-
Гомото́пия — непрерывное семейство отображений
![F_t\colon X\to Y,\; t\in [0,1]](/pictures/wiki/files/55/75cdc2141aa4aec59a3e061a0684d8f8.png) .
.Содержание
Определение
Пусть X и Y суть топологические пространства. Гомотопией называется непрерывное отображение
![F\colon[0,1]\times X\to Y](/pictures/wiki/files/49/14c0dffc35f67ba4fa92aefd60fcdf4f.png) .
.При этом значение F(t,x) чаще обозначается Ft(x).
Связанные определения
 Гомотопическая эквивалентность бублика и кружки
Гомотопическая эквивалентность бублика и кружки- Гомотопные отображения. Отображения
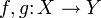 называются гомотопными или
называются гомотопными или 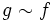 если существует гомотопия ft такая, что f0 = f и f1 = g.
если существует гомотопия ft такая, что f0 = f и f1 = g. - Гомотопическая эквивалентность топологических пространств X и Y есть пара непрерывных отображений
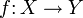 и
и 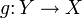 такая, что
такая, что 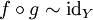 и
и 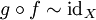 , здесь
, здесь 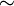 обозначает гомотопическую эквивалентность отображений. В этом случае говорят, что X и Y гомотопически эквивалентны, или X с Y имеют один гомотопический тип.
обозначает гомотопическую эквивалентность отображений. В этом случае говорят, что X и Y гомотопически эквивалентны, или X с Y имеют один гомотопический тип. - Гомотопический инвариант — это характеристика пространства, которая сохраняется при гомотопической эквивалентности топологических пространств. То есть, если два пространства гомотопически эквиваленты, то они имеют ту же характеристику. Например: связанность, фундаментальная группа, эйлерова характеристика.
- Отображение
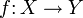 называется слабой гомотопической эквивалентностью если оно индуцирует изоморфизм гомотопических групп.
называется слабой гомотопической эквивалентностью если оно индуцирует изоморфизм гомотопических групп.
- Подпространство A топологического пространства X такое, что включение
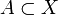 является слабой гомотопической эквивалентностью называется репрезентативным подпространством.
является слабой гомотопической эквивалентностью называется репрезентативным подпространством.
- Подпространство A топологического пространства X такое, что включение
- Если на некотором подмножестве
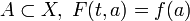 для всех t при
для всех t при 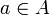 , то F называется гомотопией относительно A, а f и g гомотопными относительно A.
, то F называется гомотопией относительно A, а f и g гомотопными относительно A. - Изотопия — гомотопия топологического пространства X по топологическому пространству Y есть гомотопия
![f_t\colon X\to Y,\; t\in[0,1]](/pictures/wiki/files/102/f4bdef9106dfaaf6dc33732839307dd4.png) , в которой при любом t отображение ft является гомеоморфизмом X на
, в которой при любом t отображение ft является гомеоморфизмом X на 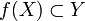 .
.
Свойства
- Гомотопия задаёт отношение эквивалентности между непрерывными отображениями
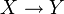
Литература
- Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. — 132 с. — ISBN 5-7036-0036-7
- Рохлин В. А., Фукс Д. Б. Начальный курс топологии. Геометрические главы. — М.: Наука, 1977
- Спеньер Э. Алгебраическая топология. — М.: Мир, 1971
См. также
- Гомотопные отображения. Отображения
Wikimedia Foundation. 2010.

