Рекурсивные функции

Рекурси́вная фу́нкция (от лат. recursio — возвращение) — это числовая функция f(n) числового аргумента, которая в своей записи содержит себя же. Такая запись позволяет вычислять значения f(n) на основе значений 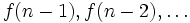$f(n-1), f(n-2),\ldots$, подобно рассуждению по индукции.Чтобы вычисление завершалось для любого n, необходимо, чтобы для некоторых n функция была определена нерекурсивно (например, для n = 0,1). Вот пример рекурсивной функции, дающей n-ое число Фибоначчи:

$F = \begin{cases} F(0)=1; \\ F(1) = 1; \\ F(n) = F(n-1) + F(n-2),\quad n > 1. \end{cases}$

Руководствуясь этой записью, мы можем вычислить F(n) для любого натурального n за конечное число шагов. Правда, по пути придется дополнительно вычислить значения 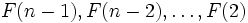$F(n-1),F(n-2),\ldots,F(2)$, В связи с этими накладными расходами полезно знать, есть ли у рекурсивной функции нерекурсивная (замкнутая) форма.

Например, рекурсивния функция:

$f = \begin{cases} f(0)=0; \\ f(n) = n + f(n-1),\quad n > 0 \end{cases}$

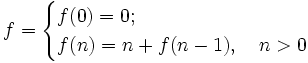
может быть переведена в замкнутую форму: 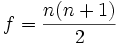$f = \frac{n(n+1)}{2}$. Замкнутая форма может быть найдена не для всех рекурсивных функций (соотношений). Для некоторых из них найдены лишь приближенные замкнутые формы. Некоторые рекурсивные соотношения, такие как факториал, считаются элементарными математическими операциями.

Рекурсивные функции играют важную роль в теории алгоритмов, так как многие алгоритмы имеют рекурсивную структуру.