РЕКУРСИВНЫЕ ФУНКЦИИ И ПРЕДИКАТЫ

РЕКУРСИВНЫЕ ФУНКЦИИ И ПРЕДИКА́ТЫ

один из важнейших для оснований математики и математич. логики классов понятий, служащих уточнениями содержат. понятий эффективно вычислимой арифметической функции и эффективно разрешимого арифметического предиката, а в конечном счете, – и лежащих в основе этих содержат. понятий интуитивных представлений об "эффективной осуществимости" и "эффективной определимости". "Эффективно осуществимым" естественно называть всякий процесс, для выполнения любого шага к-рого (в нетривиальном случае, когда этот процесс бесконечен) возможна однозначно детерминированная процедура – алгоритм; "эффективно определимым" – понятие, определимое таким образом, что для решения вопроса об отнесении к.-л. объекта к объему этого понятия также имеется алгоритм. В аналогичном смысле естественно понимать и "эффективную вычислимость" и "разрешимость". Т.о., уточнения всех упомянутых представлений об "эффективности" были вызваны к жизни тем же конструктивным подходом к формулировке и решению (логико-) математич. задач, к-рым обусловлены и различные уточнения понятия алгоритма. Общее определение "(эффективной) вычислимости" естественно было искать по отношению к функциям, определенным на возможно более п р о с т о й в к.-л. отношении области, носящей в то же время настолько общий характер, чтобы перенесение выработанных для нее понятий и методов на функции, определенные на более сложных областях, не представляло бы принципиальных затруднений. Подходящей в обоих этих отношениях областью является натуральный ряд чисел 0, 1, 2..., исходя из к-рого строятся и более сложные и богатые числовые классы: классы целых, рациональных, действительных и комплексных чисел (см. Э. Ландау, Основы анализа, пер. с нем., М., 1947). И обратно, любая вычислит. задача сводится (с любой, в принципе, заданной точностью) к задаче вычисления нек-рой функции натурального аргумента (или конечного набора натуральных аргументов), принимающей натуральные значения (именно такие функции выше подразумевались под "арифметическими"). Эта в известном смысле "универсальность" класса арифметич. функций имеет не только принципиально-гносеологич. значение – она лежит в основе программирования самых разнообразных задач на универсальных цифровых (электронных) машинах, в свою очередь расширяющего наши познават. возможности. "Генетический" способ построения натурального ряда, состоящий в переходе от любого натурального числа n к непосредственно следующему за ним числу n', выраженный в принципе математической индукции, наводит на мысль и об универсальном (для арифметики) характере т.н. определений по индукции арифметич. функций (и предикатов). Примерами таких определений по индукции, или, как их называют, рекурсивных (от лат. recurso – возвращаюсь) определений, служат определение функции φ (a, n) = a + n (операции сложения) с помощью аксиом

φ (a,0)=а (*)

и

φ (a, n')=(φ(a, n))', (**)

позволяющее вычислить значение φa (n) = φ (a, n) = a + n для любой пары натуральных чисел а и n, и аналогичная пара аксиом для умножения.

[Рекурсивные определения не следует путать с индуктивными определениями; такая путаница обусловлена как сходством терминов, так и родством этих процедур по существу: последние – в том случае, когда они служат определением к.-л. области объектов, при условии, что объекты, порожденные различными путями, обязательно различны, – являются необходимой предпосылкой для рекурсивных определений функций или предикатов, определяемых на к.-л. подмножестве этой области (см. Определение, раздел Рекурсивные и индуктивные определения)]. Т. Сколем (1920) показал, что с помощью такого рода "рекурсий", в известном смысле свойственных самой природе натурального ряда, можно определить осн. понятия арифметики. Существенно иметь в виду, что по крайней мере часть таких "схем рекурсий" – во всяком случае формулы (*) и (**) – приходится включать в аксиоматич. арифметику именно в качестве аксиом, не поддающихся элиминированию (устранению) из системы без ее существ. ослабления; то же относится к упоминаемой ниже общей схеме примитивной рекурсии (принятие к-рой непременно предполагает принятие принципа математич. индукции в метатеории). Расширения системы за счет перехода от n-местных функций к (n+1)-местным (в т.ч. и столь "очевидные", как произведенное выше отождествление одноместной функции φa (n), зависящей от параметра a, с двуместной функцией φ (a, n)), также должны быть явно оговорены при формулировке арифметич. формализма. Все эти оговорки, необходимые особенно в связи с идущим еще со времен Пеано ошибочным мнением, согласно к-рому корректность рекурсивных определений есть автоматич. следствие аксиомы индукции), конечно, не снимают проблемы обоснования теории Р. ф. и п., т.е. поиска убедительных, свободных от круга (и не использующих, как это обычно делается, теоретико-множеств. допущений) доводов в пользу существования в натуральном ряду любых функций, определяемых рекурсивными схемами. (Весьма трудный анализ такого рода проблематики, практически не затрагиваемый в большинстве работ по теории Р. ф. и п., явился в последние годы темой рассмотрения т.н. ультраинтуиционизма.) Т.о., назрела идея положить "рекурсии" в основу точного и общего определения понятия "вычислимой" функции. Эта идея, реализованная первоначально в виде т.н. схемы примитивной рекурсии (см. ниже схему II), была в явной форме впервые сформулирована Гёделем (1931). При определении новых функций естественно, конечно, использовать уже имеющиеся (определенные) ранее функции путем явного определения через последние, т.е. посредством операции подстановки значений одних известных функций в другие, ранее определенные функции, описываемой с помощью т.н. схемы регулярной суперпозиции функций (см. ниже схему I). В качестве исходных при этом обычно выбирают простейшие арифметич. функции: (1) функцию φ (x1, x2, ..., xn) = 0 (n=0,1,...), равную тождественно константе 0, (2) функцию "(непосредственного) следования за" φ (x) = x´ (т.е. именно те первоначальные функции, с помощью к-рых строится натуральный ряд), а также (3) функции φ (х1, х2, ..., xi, ..., xn) = xi (i = 1, 2, ..., n; n = 1, 2, ...), равные значению одного из своих аргументов. Определяемые на этой основе (с помощью приводимых ниже схем I и II) функции наз. примитивно-рекурсивными функ-ц и я м и ( П Р Ф). Класс ПРФ, охватывающий наиболее часто встречающиеся арифметические функции, не охватывает, однако, всех функций, которые можно вычислить для любых значений аргументов, – еще в 1928, т.е. еще до появления термина "рекурсивные функции", нем. математик В. Аккерман построил пример "вычислимой" функции, не являющейся в то же время ПРФ. Между тем во всех исследованиях, посвященных определению понятия вычислимой функции (ВФ), все время имелся в виду (вначале неявно) тезис (т.н. тезис Чёрча), согласно к-рому такое определение должно охватывать все "мыслимые" виды "вычислимости", т.е. чтобы полученное определение отвечало т.н. осн. гипотезе теории ВФ (а поскольку "вычислимость" – это не что иное, как существование алгоритма вычисления, то, по существу, и осн. гипотезе теории алгоритмов; см. Алгоритм, Массовая проблема). Поиски такого общего определения ВФ (в ходе к-рых были найдены многочисл. виды определяющих схем более общего вида, чем схема примитивной рекурсии, но также удовлетворяющие требованию "эффективной вычислимости", причем одни из них, как, напр., т.н. "возвратная рекурсия", требующая для определения значения функции в точке n не только знания ее значения в точке n – 1, но, возможно, и при других меньших значениях аргумента, оказались сводимыми к этой схеме, а другие, подобно "двойной" или "одновременной" рекурсии, по разл. переменным n и m, – не сводимыми) привели франц. математика Ж. Эрбрана (1931) и К. Гёделя (1934) к формулировке фундаментального понятия обще-рекурсивной функции ( О Р Ф), по отношению к которому и был в 30-х гг. выдвинут тезис Чёрча. Следует отметить, что понятие ОРФ явилось лишь одним из многих уточнений понятия ВФ. Эквивалентность всех этих уточнений, указывающая на важность класса функций, характеризуемых любым из них, служит одним из серьезнейших доводов в пользу тезиса Чёрча.

Требование, чтобы функция n натуральных аргументов была определена для каждого набора из n натуральных чисел, оказывается часто слишком обременительным ограничением. В 1938 С. К. Клини ввел понятие частично-рекурсивной функции ( Ч Р Ф) – функции, определенной не для всех натуральных значений аргументов, а лишь на нек-рых подмножествах натурального ряда, а в остальном удовлетворяющей определению ОРФ. Клини доказал также одну из важнейших теорем теории рекурсивных функций – теорему о нормальной форме для ОРФ (и ЧРФ), позволившую существенно упростить первоначально очень громоздкие определения ОРФ и ЧРФ.

Эта теорема формулируется след. образом: для каждого натурального числа n существуют такие две ПРФ U (y) и τn (z, х 1, х2, ..., х n, у), что для любой ОРФ φ (x1, x2, ..., хn) существует такое (натуральное) число е, что

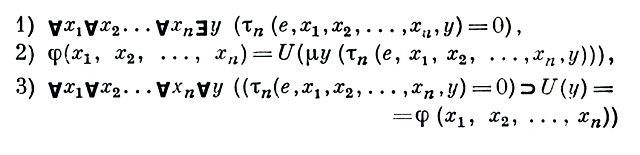(где μ - оператор, означающий "наименьшее число такое, что..."). Если в формулировке этой теоремы отбросить (1) и заменить слова "ОРФ" на "ЧРФ", то получится теорема о нормальной форме для ЧРФ. Значение этой теоремы состоит в том, что она дает стандартный способ получения любой ЧРФ из двух заранее выбранных ПРФ. Упрощенное с помощью этой теоремы определение ЧРФ выглядит след. образом: ЧРФ наз. функция, к-рая может быть определена, исходя из "базисных" функций (1) - (3), посредством конечного числа применений след. схем образования новых функций φ из ранее построенных функций f, g, h: I. Подстановка (или регулярная суперпозиция) функций f1 (х 1, х2, ..., хm), f2 (x1, x2, ..., xm), ..., fk (x1, x2, ..., х m) на место аргументов функции f0 (х 1, х2, ..., хk) - φ (x1, х2, ..., хm) = f0 (f1 (х 1, х2, ..., х m), f2 (x1, х2, , xm), ..., fk (х 1, x2, ..., хm)).

II. Схемы примитивной рекурсии - определение k-местной функции φ посредством известных ранее (k - 1)-местной функции g (при k=1g - константа, как в приведенном выше примере с функцией сложения натуральных чисел) и (k + 1)-местной функции h:

φ (x1, х2, ..., xk-1, 0) = g (x1, х2, ..., xk-1), φ (x1, x2, ..., xk-1, n´) = h (x1, x2, ...,xk-1, n, φ (x1, ..., xk-1, n)).

III. Операция взятия наименьшего числа - построение по функции f (x1, x2, ..., ..., xk, xk-1) (k≥1) функции φ (х 1, х2, ..., хk), значение к-рой для аргументов х 1, х2, ..., хk равно такому у, что f (х 1, х2, ..., хk, у) = 0, а для всех z < у значения f (x1, x2, ..., хk, z) определены и не равны нулю (если же такого у не существует, то φ для данных х 1, х2, ..., хk не определена) - φ (х 1, х2, ..., хk) = μy(f (x1, x2, ..., хk, y) = 0).

Всюду определенная ЧРФ, т.е. такая, что при каждом применении схемы III имеет место Vx1...VхkBy(f (x1, x2, ..., хk, y) = 0) наз. ОРФ.

Обще-рекурсивная функция, определимая лишь с помощью схем I и II, наз. ПРФ. Т.о., всякая ПРФ есть ОРФ, а ОРФ есть ЧРФ, но не обратно; легко строятся примеры ОРФ, не являющихся ПРФ, а понятие ЧРФ существенно шире понятия ОРФ – легко доказать, что имеются такие ЧРФ, что не существует никакого способа так доопределить их на той части натурального ряда, на к-рой они не определены, чтобы в результате получилась ОРФ. Естеств. параллелизм, устанавливаемый между понятиями функции и предиката посредством т.н. представляющих (или характеристических) функций арифметич. предикатов (т.е. функций, принимающих значения 0 для всех наборов аргументов, для к-рых соответствующий предикат истинен, и значение 1 для всех наборов аргументов, для к-рых этот предикат ложен), приводит к понятиям примитивно-, обще- и частично-рекурсивного предиката. Примитивная, общая и частичная рекурсивность предикатов сохраняется при применении к ним операций логики высказываний, а также ограниченных кванторов (см. Квантор) и ограниченного оператора μ (см. выше). Интерес к этим классам предикатов обусловлен, как и в случае функций, их "эффективно разрешимым" характером.

Как по отношению к функциям, так и по отношению к предикатам, рассматривают также относит. рекурсивность (примитивную, общую или частичную) – в этих случаях вместо зафиксированных выше конкретных исходных функций выбирают к.-л. др. функции (и говорят о рекурсивности относительно этих функций), оставляя схемы I – III (или часть из них) без изменений.

В математич. логике рассматриваются и другие, более специальные виды Р. ф. и п., а также их обобщения, в частности на область т.н. "конструктивных трансфинитных чисел", включающую натуральный ряд в качестве подмножества. Кроме того, аналогичная терминология употребляется и по отношению к множествам (см. Разрешимое и перечислимое множества).

Теория Р. ф. и п. имеет обширные применения в основаниях математики, важнейшими из к-рых являются т.н. арифметизация синтаксиса формальных систем и основанное на ней использование понятий и аппарата этой теории в доказательствах теорем Гёделя о неполноте арифметики (см. Метатеория, Полнота). Вместе с тем с помощью определений, по форме аналогичных рекурсивным, можно преодолеть круги в "порочных" определениях эмпирич. наук. Необходимо заметить, что все изложенные выше концепции и результаты базировались (как правило, в неявной форме) на ряде предположений традиц. математики, наиболее существенными из к-рых являются: допущение о том, что натуральный ряд замкнут относительно любой ПРФ (т.е., что определение любой ПРФ допускает неограниченное число раз применять его начиная с любого натурального числа, причем на любой стадии этого процесса результат также будет натуральным числом); признание однозначной (с точностью до изоморфизма) определенности натурального ряда с помощью аксиом Пеано. При всей традиционности такого рода допущений они уязвимы для критики с позиций ультраинтуиционизма (см. A. S. Ésénine-Volpine, Le programme ultraintuitionniste des fondements des mathématiques, в кн.: Infinitistic methods, Warsz., 1961), к-рая ведет к существ. пересмотру как ряда исходных концепций теории Р. ф. и п., так и нек-рых из ее важнейших результатов, в т.ч. теоремы Гёделя (1931), согласно к-рой каждый примитивно-рекурсивный предикат может быть явно выражен в терминах постоянных и переменных натуральных чисел, функций следования, сложения и умножения, предиката равенства и операций узкого классич. исчисления предикатов, т.е. как раз той теоремы, к-рая оправдывает конечность системы аксиом, принимаемой обычно для формализации арифметики, и позволяет не включать в эту систему схемы всевозможных ПРФ. О др. методологич. вопросах, связанных с понятиями Р. ф. и п. и ВФ, см. Алгоритм, а также лит. при этой статье.

Лит.: Петер Р., Рекурсивные функции, пер. с нем., М., 1954 (имеется библ.); Клини С. К., Введение в метаматематику, пер. с англ., М., 1957, ч. 3 (имеется библ.); Εсенин-Вольпин А. С., Анализ потенциальной осуществимости, в сб.: Логические исследования, М., 1959; Успенский В. Α., Лекции о вычислимых функциях, М., 1960; Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965.

Ю. Гастев, И. Шмаин. Москва.

Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.