- Пфафиан
-
Пфаффиан — характеристика кососимметричной матрицы.
Определитель кососимметричной матрицы можно представить как квадрат некоторого многочлена от элементов матрицы. Этот многочлен называется пфаффиан. Как и определитель, пфаффиан не обнуляется только для
 кососимметричных матриц и в этом случае является многочленом степени n от элементов матрицы.
кососимметричных матриц и в этом случае является многочленом степени n от элементов матрицы.Содержание
Примеры
Стандартное определение
Пусть Π обозначает множество всех разбиений
 на неупорядоченные пары (всего существует (2n − 1)!! таких разбиений). Разбиение
на неупорядоченные пары (всего существует (2n − 1)!! таких разбиений). Разбиение  , может быть записано
, может быть записаногде ik < jk и
 . Пусть
. Пустьобозначает соответственную перестановку, определим знак sgn(α) как знак перестановки sgn(π). Нетрудно видеть что sgn(α) не зависит от выбора π.
Пусть A = {aij} обозначает
 кососимметричную матрицу. Для разбиения α определим
кососимметричную матрицу. Для разбиения α определимТеперь можно определить пфаффиан A как
Пфаффиан
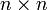 кососимметричной матрицы для нечётного n является нулём по определению.
кососимметричной матрицы для нечётного n является нулём по определению.Альтернативное определение
Для
 кососимметричной матрицы A = {aij} рассмотрим бивектор:
кососимметричной матрицы A = {aij} рассмотрим бивектор:где
 есть стандартный базис в
есть стандартный базис в  . Тогда пфаффиан определяется следующим уравнением:
. Тогда пфаффиан определяется следующим уравнением:где
 обозначает внешнее произведение n копий ω.
обозначает внешнее произведение n копий ω.Свойства
Для
 кососимметричной матрицы A и для произвольной
кососимметричной матрицы A и для произвольной  матрицы B:
матрицы B:- Pf(A)2 = det(A)
- Pf(BABT) = det(B)Pf(A)
- Pf(λA) = λnPf(A)
- Pf(AT) = ( - 1)nPf(A)
- Для блок-диагональной матрицы
- Для произвольной
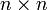 матрицы M:
матрицы M:
История
Термин «пфаффиан» был введён Кэли и назван в честь немецкого математика Йохана Фридриха Пфаффа (нем.).
Литература
- М. Н. Вялый, Пфаффианы или искусство расставлять знаки... — Сборник «Математическое Просвещение» Выпуск 9 (2005 год)
Wikimedia Foundation. 2010.











