- Приведенная стоимость
-
Дисконтированная стоимость выражает стоимость будущих потоков платежей в значении текущих потоков платежей. Определение дисконтированной стоимости широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить какой объем финансовых вложений намерен сделать инвестор для получения определенного денежного потока через заданный срок. Дисконтированная стоимость будущего потока платежей является функцией:
- инфляции,
- срока через который ожидается будущий поток платежей,
- риска связанного с данным будущим потоком платежей,
- стоимости денег с учетом фактора времени
- других факторов.
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Содержание
Объяснение
Ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность чем 100 рублей, которые имеются в наличии. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет. Кроме того, на имеющиеся в наличии 100 руб. можно приобрести товар, который через пять лет будет иметь более высокую цену в следствие инфляции. Следовательно 100 руб. через пять лет не позволят приобрести тот же товар. В данном примере показатель дисконтированной стоимости позволяет вычислить сколько на сегодняшний день стоят 100 руб. которые будут получены через пять лет.
Вычисление
где
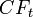 - поток платежей полученный через
- поток платежей полученный через 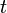 лет,
лет, 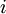 - ставка дисконтирования определенная исходя из вышеперечисленных факторов,
- ставка дисконтирования определенная исходя из вышеперечисленных факторов, 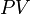 - дисконтированная стоимость будущего потока платежей
- дисконтированная стоимость будущего потока платежей 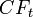 .
.Для того чтобы получить через
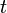 лет сумму равную
лет сумму равную 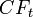 , при том что инфляция, риск и др. определяют ставку дисконтирования равную
, при том что инфляция, риск и др. определяют ставку дисконтирования равную 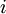 , инвестор согласен вложить сегодня сумму равную
, инвестор согласен вложить сегодня сумму равную 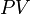 .
.Дисконтированная стоимость серии потоков платежей и аннуитетных платежей
Дисконтированная стоимость серии потоков платежей равна сумме дисконтированных стоимостей каждого из составляющих потоков платежей. Так, дисконтированная стоимость серии потоков платежей
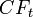 получаемых каждый год в течении периода
получаемых каждый год в течении периода 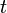 лет вычисляется по следующей формуле:
лет вычисляется по следующей формуле:Если аннуитетные платежи имеют одинаковую величину, то эту формулу можно применять и для вычисления дисконтированной стоимости аннуитетных платежей.
Для большого
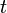 , формулу можно упростить посредством сложения геометрических рядов[1]. Каждый член геометрического ряда является дисконтированной стоимостью очередного аннуитетного платежа. Дисконтированная стоимость одинаковых по величине аннуитетных платежей вычисляется по формуле:
, формулу можно упростить посредством сложения геометрических рядов[1]. Каждый член геометрического ряда является дисконтированной стоимостью очередного аннуитетного платежа. Дисконтированная стоимость одинаковых по величине аннуитетных платежей вычисляется по формуле:![PV \,=\,\frac{CF}{i}\cdot[1-\frac{1}{\left(1+i\right)^n}]](/pictures/wiki/files/48/0489f3993810c428f5a41fd765b9d97f.png) ,
,
где
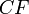 - аннуитетный платеж осуществляемый
- аннуитетный платеж осуществляемый 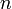 раз,
раз, 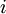 - ставка дисконтирования,
- ставка дисконтирования, 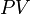 - дисконтированная стоимость аннуитетных платежей
- дисконтированная стоимость аннуитетных платежей 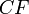 .
.Дисконтированная стоимость аннуитетных платежей с ростом
Если денежные потоки аннуитетных платежей растут в (1+g) раз (ставка роста равна g), то их дисконтированная стоимость вычисляется по формуле:
где
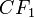 - аннуитетный платеж осуществляемый в первый период,
- аннуитетный платеж осуществляемый в первый период, 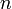 - число периодов,
- число периодов, 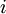 - ставка дисконтирования,
- ставка дисконтирования, 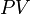 - дисконтированная стоимость аннуитетных платежей.
- дисконтированная стоимость аннуитетных платежей.Формула получается вычитанием формулы для расчета дисконтированной стоимости перпетуитета начинающегося в году n из упрощенной формулы модели Гордона.
Дисконтированная стоимость перпетуитетов (бессрочных аннуитетов)
Исходя из формулы расчета дисконтированной стоимости аннуитетных платежей, можно получить формулу для дисконтированной стоимости перпетуитетов(бессрочных аннуитетов). Когда значение
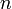 стремится к бесконечности, часть формулы
стремится к бесконечности, часть формулы 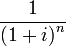 , стремится к нулю. При таких условиях формула для перпетуитетов будет иметь следующий вид:
, стремится к нулю. При таких условиях формула для перпетуитетов будет иметь следующий вид: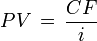 .
.
Дисконтированная стоимость бессрочных ценных бумаг с растущими платежами, например акции c увеличивающимися дивидендными доходами рассчитывается по модели Гордона
References
- ↑ Единая коллекция цифровых образовательных ресурсов. Проверено 18 мая 2009.
Wikimedia Foundation. 2010.

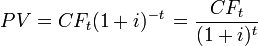
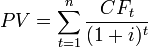
![PV\,=\,{CF_1 \over (i-g)}\left[ 1- \left({1+g \over 1+i}\right)^n \right]](/pictures/wiki/files/97/a8efeb7f5f8df4c8b2108f20450f8393.png)