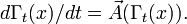- Поток вектора
-
В математике поток векторного поля используется для двух различных понятий:
1. Поток векторного поля через гиперповерхность (см. ниже),
2. Поток векторного поля
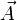 — однопараметрическое семейство диффеоморфизмов Γt определямых дифференциальным уравнением
— однопараметрическое семейство диффеоморфизмов Γt определямых дифференциальным уравнениемПоток векторного поля через гиперповерхность
Поток векторного поля через гиперповерхность — поверхностный интеграл второго рода по поверхности S. По определению
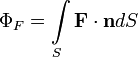
где
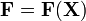 — векторное поле (вектор-функция векторного аргумента — точки пространства),
— векторное поле (вектор-функция векторного аргумента — точки пространства), 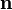 — единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — т.е. для дифференцируемой поверхности — так, чтобы
— единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — т.е. для дифференцируемой поверхности — так, чтобы 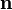 было непрерывно; для неориентируемой поверхности это не важно, т.к. поток через неё всегда ноль), dS — элемент поверхности.
было непрерывно; для неориентируемой поверхности это не важно, т.к. поток через неё всегда ноль), dS — элемент поверхности.- В трёхмерном случае
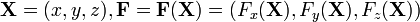 , а гиперповерхность - есть обычная двумерная поверхность.
, а гиперповерхность - есть обычная двумерная поверхность.
Иногда, особенно в физике, применяется обозначение
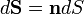
тогда поток записывается в виде
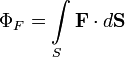
Физическая интерпретация
Пусть движение несжимаемой жидкости единичной плотности в пространстве задано векторным полем скорости течения
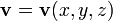 . Тогда масса жидкости, которая протечёт за единицу времени через поверхность S, будет равна потоку векторного поля
. Тогда масса жидкости, которая протечёт за единицу времени через поверхность S, будет равна потоку векторного поля 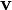 через поверхность S.
через поверхность S.См. также
Wikimedia Foundation. 2010.