Построение выпуклой оболочки методом разделяй и властвуй

Построение выпуклой оболочки методом «разделяй и властвуй» — алгоритм построения выпуклой оболочки.

Описание

Дано множество S, состоящее из N точек.

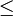1. Если |S| $\leq$ k₀ (k₀ — некоторое небольшое целое число), то построить выпуклую оболочку одним из известных методов и остановиться, иначе перейти к шагу 2.
2. Разобьем исходное множество S произвольным образом на два примерно равных по мощности подмножества S₁ и S₂ (пусть S₁ содержит N/2 точек, а S₂ содержит N N/2 точек).
3. Рекурсивно находим выпуклые оболочки каждого из подмножеств S₁ и S₂.
4. Строим выпуклую оболочку исходного множества как выпуклую оболочку объединения двух выпуклых многоугольников CH(S₁) и CH(S₂).

Поскольку: CH(S) = CH(S1 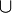$\cup$ S2) = CH(CH(S₁) 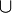$\cup$ CH(S₂)), сложность этого алгоритма является решением рекурсивного соотношения T(N) 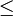$\leq$ 2T(N/2) + f(N), где f(N) — время построения выпуклой оболочки объединения двух выпуклых многоугольников, каждый из которых имеет около N/2 вершин. Далее будет показано, что T(N) = O(N logN).

Определения

Опорной прямой к выпуклому многоугольнику P называется прямая l, проходящая через некоторую вершину многоугольника P таким образом, что все внутренние точки многоугольника лежат по одну сторону от прямой l.

Реализация

1. Найдём некоторую внутреннюю точку A многоугольника P1 (например, центроид трёх любых вершин P1). Такая точка А будет внутренней точкой CH(P1 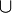$\cup$ P2).
2. Возможно два случая:
   1. Точка A не является внутренней точкой многоугольника P2. Проводим две опорные прямые для многоугольника P1, проходящие через точку А. Эти опорные прямые проходят через вершины В и С многоугольника P2.Все точки внутри треугольника АВС не принадлежат границе выпуклой оболочки CH(P1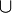$\cup$P2). Все остальные точки упорядочиваем по полярному углу относительно центра А, слиянием двух упорядоченных списков вершин за время O(N₁) + O(N₂) = O(N), а затем применяем к полученному списку метод обхода Грэхема, требующий лишь линейное время. Опорные прямые к многоугольнику P2 могут быть построены исходя из следующих соображений. Прямая АP_i, где P_i — некоторая вершина многоугольника P2, является опорной к P2 в том и только в том случае, если ребра (P_{i − 1}, P_i) и (P_i, P_{i + 1}) лежат в одной полуплоскости, ограниченной этой прямой. Нетрудно видеть, что для построения опорных прямых AB и AC требуется в худшем случае один обход вершин многоугольника P2, то есть время O(N₂).
   2. Точка А является внутренней точкой многоугольника P2 . Упорядочиваем вершины обоих многоугольников относительно центра А, сливая два упорядоченных списка вершин P1 и P2 за O(N).
3. Теперь к полученному списку вершин можно применить метод обхода Грэхема, который выполняется за линейное время. Теперь получена выпуклая оболочка объединения выпуклых многоугольников P1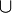$\cup$P2.

Сложность алгоритма

Проверка принадлежности точки A многоугольнику P2 выполняется за время O(N₂). В каждом из двух рассмотренных случаев время выполнения соответствующего алгоритма равно O(N). Таким образом общая сложность алгоритма построения выпуклой оболочки объединения двух выпуклых многоугольников составляет O(N). Отсюда заключаем, что в соотношении T(N) 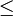$\leq$ 2T(N/2) + f(N): f(N) = O(N), значит решением соотношения является T(N) = O(N logN), что и определяет сложность алгоритма.

Ссылки

• http://www.cs.umd.edu/~samir/754/kshand.ps(англ.)