Парадокс парикмахера

Парадокс Рассела — открытая в 1903 году Бертраном Расселом и позднее независимо переоткрытая Э. Цермело теоретико-множественная антиномия, демонстрирующая несовершенство языка наивной теории множеств Г. Кантора, а не ее противоречивость.

Антиномия Рассела формулируется следующим образом:

Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли K само себя в качестве элемента? Если да, то, по определению K, оно не должно быть элементом K — противоречие. Если нет — то, по определению K, оно должно быть элементом K — вновь противоречие.

Противоречие в антиномии Рассела возникает из-за использования в рассуждении понятия множества всех множеств и представления о возможности неограниченного применения законов классической логики при работе с множествами. Для преодоления этой антиномии было предложено несколько путей. Наиболее известный состоит в предъявлении для теории множеств непротиворечивой формализации 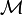$\mathcal M$, по отношению к которой являлись бы допустимыми все «действительно нужные» (в некотором смысле) способы оперирования с множествами. В рамках такой формализации утверждение о существовании множества всех множеств было бы невыводимым.

Действительно, допустим, что множество U всех множеств существует. Тогда, согласно аксиоме выделения, должно существовать и множество K, элементами которого являются те и только те множества, которые не содержат себя в качестве элемента. Однако предположение о существовании множества K приводит к антиномии Рассела. Следовательно, ввиду непротиворечивости теории 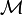$\mathcal M$, утверждение о существовании множества U невыводимо в этой теории, что и требовалось доказать.

В ходе реализации описанной программы «спасения» теории множеств было предложено несколько возможных её аксиоматизаций (теория Цермело — Френкеля ZF, теория Неймана — Бернайса — Гёделя NBG, и т. д.), однако ни для одной из этих теорий до настоящего момента не найдено доказательства непротиворечивости. Более того, как показал Гёдель, разработав ряд теорем о неполноте, такого доказательства не может существовать (в некотором смысле).

Другой реакцией на открытие парадокса Рассела явился интуиционизм Л. Э. Я. Брауэра.

Ошибочно считают, что этот парадокс демонстрирует противоречивость теории множеств Г.Кантора. Для опровержения этих взглядов Н. Вавилов ^[1] приводит следующий парадокс - "Парадокс Пиглета":

Пусть n - такое целое число, которое одновременно больше и меньше нуля. Тогда n в том и только том случае является положительным, когда оно является отрицательным.

Очевидно, что из него следует лишь несуществование предположенного нами числа n, а не противоречивость теории чисел в целом - этот же метод используется в доказательствах от противного.

Структура данного парадокса идентична структуре парадокса Рассела, что позволяет делать выводы лишь о противоречивости понятия "множество всех множеств", но не теории множеств в целом.

Варианты формулировок

Существует много популярных формулировок этого парадокса. Одна из них традиционно называется парадоксом брадобрея и звучит так:

Одному деревенскому брадобрею приказали «брить всякого, кто сам не бреется, и не брить того, кто сам бреется», как он должен поступить с собой?

Еще один вариант:

В одной стране вышел указ: «Мэры всех городов должны жить не в своем городе, а в специальном Городе мэров», где должен жить мэр Города мэров?

И ещё один:

Некая библиотека решила составить библиографический каталог, в который входили бы все те и только те библиографические каталоги, которые не содержат ссылок на самих себя. Должен ли такой каталог включать ссылку на себя?

Литература

• Р. Курант, Г. Роббинс. Что такое математика? гл. II, § 4.5
• Мирошниченко П.Н. Что же разрушал парадокс Рассела в системе Фреге? // Современная логика:проблемы теории,истории и применения в науке. СПб.,2000. С.512-514.
• Катречко С.Л. Расселовский парадокс брадобрея и диалектика Платона -Аристотеля //Современная логика:проблемы теории,истории и применения в науке. СПб.,2002. С.239-242.

Примечания

1. ↑ Вавилов Н.А. Не совсем наивная теория множеств / Н.А. Вавилов. – Электрон. дан. – URL: http://www.math.spbu.ru/user/valgebra/set-int.pdf (дата обращения: 11.04.2009)