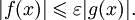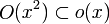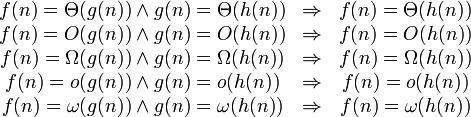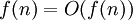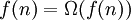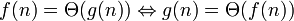О-большое

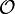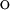«O» большое и «o» малое ($\mathcal{O}$ и $\mathrm{o}\!\,$) — математические обозначения для сравнения асимптотического поведения функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также при оценке сложности алгоритмов. В частности, фраза «сложность алгоритма есть O(n!)» означает, что при больших n время работы алгоритма (или общее количество операций) не более чем C · n!, где C — некая положительная константа (обычно в качестве параметра n берут объём входной информации алгоритма).

Определения

Пусть f(x) и g(x) — две функции, определенные в некоторой проколотой окрестности точки x₀, причем в этой окрестности g не обращается в ноль. Говорят, что:

• f является «O» большим от g при $x\to x_0$, если существует константа C > 0, что для всех x из некоторой окрестности точки x₀ имеет место неравенство

  $|f(x)| \leqslant C |g(x)|$;

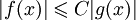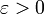• f является «о» малым от g при $x\to x_0$, если для любого $\varepsilon>0$ найдется такая проколотая окрестность 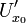$U_{x_0}'$ точки x₀, что для всех 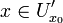$x\in U_{x_0}'$ имеет место неравенство

  $|f(x)| \leqslant \varepsilon |g(x)|.$

Иначе говоря, в первом случае отношение | f | / | g | в окрестности точки x₀ ограничено сверху, а во втором оно стремится к нулю при $x\to x_0$.

Обозначение

Обычно выражение «f является „O“ большим („о“ малым) от g» записывается с помощью равенства f(x) = O(g(x)) (соответственно, f(x) = o(g(x))).

Это обозначение очень удобно, но требует некоторой осторожности при использовании (а потому в наиболее элементарных учебниках его могут избегать). Дело в том, что это не равенство в обычном смысле, а несимметричное отношение.

В частности, можно писать

f(x) = O(g(x)) (или f(x) = o(g(x))),

но выражения

O(g(x)) = f(x) (или o(g(x)) = f(x))

бессмысленны.

Другой пример: при x → 0 верно, что

O(x²) = o(x),

но неверно, что

o(x) = O(x²).

Вместо знака равенства методологически правильнее было бы употреблять знаки принадлежности и включения, понимая O( ) и o( ) как обозначения для множеств функций, то есть используя запись в форме

x² + x³ ∈ O(x²)

или

$\mathop O(x^2)\subset o(x)$

вместо, соответственно,

x² + x³ = O(x²)

и

$\mathop O(x^2) = o(x)$

Однако на практике такая запись встречается крайне редко, в основном в простейших случаях.

При использовании данных обозначений должно быть явно оговорено (или очевидно из контекста), о каких окрестностях (одно- или двусторонних; содержащих целые, вещественные или комплексные числа и т. п.) и о каких допустимых множествах функций идет речь (поскольку такие же обозначения употребляются и применительно к функциям многих переменных, к функциям комплексной переменной, к матрицам и др.).

Другие подобные обозначения

Для функций f(n) и g(n) при n → n₀ используются следующие обозначения:

Обозначение	Интуитивное объяснение	Определение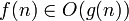
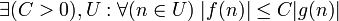
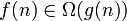
$f(n) \in O(g(n))$	f ограничена сверху функцией g (с точностью до постоянного множителя) асимптотически	$\exists (C>0), U : \forall (n \in U) \; |f(n)| \leq C|g(n)|$
$f(n) \in \Omega(g(n))$	f ограничена снизу функцией g (с точностью до постоянного множителя) асимптотически	$\exists (C>0), U : \forall (n \in U) \; C|g(n)| \leq |f(n)|$
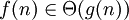
$f(n) \in \Theta(g(n))$	f ограничена снизу и сверху функцией g асимптотически	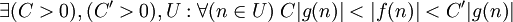$\exists (C>0), (C'>0), U : \forall (n \in U) \; C|g(n)| < |f(n)| < C'|g(n)|$
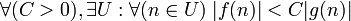
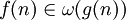
$f(n) \in o(g(n))$	g доминирует над f асимптотически	$\forall (C>0) ,\exists U : \forall(n \in U) \; |f(n)| < C|g(n)|$
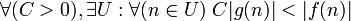
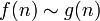
$f(n) \in \omega(g(n))$	f доминирует над g асимптотически	$\forall (C>0) ,\exists U : \forall(n \in U) \; C|g(n)| < |f(n)|$
$f(n) \sim g(n)\!$	f эквивалентна g асимптотически	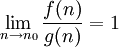$\lim_{n \to n_0} \frac{f(n)}{g(n)} = 1$

где U — проколотая окрестность точки n₀.

Основные свойства

Транзитивность

• $\begin{matrix}f(n)=\Theta(g(n)) \land g(n)=\Theta(h(n)) & \Rightarrow & f(n) = \Theta (h(n)) \\ f(n)=O(g(n)) \land g(n)=O (h(n)) & \Rightarrow & f(n) = O (h(n)) \\ f(n)=\Omega(g(n)) \land g(n)=\Omega(h(n)) & \Rightarrow & f(n) = \Omega(h(n)) \\ f(n)=o(g(n)) \land g(n)= o (h(n)) & \Rightarrow & f(n) = o (h(n)) \\ f(n)=\omega(g(n)) \land g(n)=\omega(h(n)) & \Rightarrow & f(n) = \omega(h(n))\end{matrix}$

Рефлексивность

• $f(n)=\Theta(f(n))\!$
• $f(n)=O(f(n))\!$
• $f(n)=\Omega(f(n))\!$

Симметричность

• $f(n)=\Theta(g(n)) \Leftrightarrow g(n)=\Theta(f(n))$

Перестановочная симметрия

$\begin{matrix} f(n)= O(g(n)) & \Leftrightarrow & g(n)=\Omega(f(n)) \\ f(n)= o(g(n)) & \Leftrightarrow & g(n)=\omega(f(n)) \end{matrix}$

Другие

• o(f) = const × o(f); O(f) = const × O(f);
• o(f) = o(const × f); O(f) = O(const × f);
• o(f) = O(f);
• o(f) + o(f) = o(f); o(f) + O(f) = O(f); O(f) + O(f) = O(f);
• O(f) × O(g) = O(fg); o(f) × O(g) = o(fg); o(f) × o(g) = o(fg);
• O(O(f)) = O(f);
• o(o(f)), o(O(f)), O(o(f)) = o(f);
• O(-f) = O(f)

Асимптотические обозначения в уравнениях

• Если в правой части уравнения находится только асимптотическое обозначение (например n = O(n²)), то знак равенства обозначает принадлежность множеству (n ∈ O(n²)).
• Если в уравнении асимптотические обозначения встречается в другой ситуации, они рассматриваются как подставляемые взамен их некоторые функции. Например, при x → 0 формула e^x − 1 = x + o(x) обозначает, что e^x − 1 = x + f(x), где f(x) — функция, о которой известно только то, что она принадлежит множеству o(x). Предполагается, что таких функций в выражении столько, сколько раз встречаются в нём асимптотические обозначения. Например, 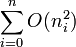  $\sum_{i=0}^nO(n_i^2)$   — содержит только одну функцию из класса O(n²).
• Если асимптотические обозначения встречаются в левой части уравнения, используют следующее правило:
  какие бы мы функции не выбрали (в соответствии с предыдущим правилом) взамен асимптотических обозначений в левой части уравнения, можно выбрать функции вместо асимптотических обозначений (в соответствии с предыдущим правилом) в правой части так, что уравнение будет правильным.
  Например, запись x + o(x) = O(x) обозначает, что для любой функции f(x) ∈ o(x), существует некоторая функция g(x), такая что выражение x + f(x) = g(x) — верно для всех x.
• Несколько таких уравнений могут быть объединены в цепочки. Каждое из уравнений в таком случае следует интерпретировать в соответствии с прдыдущим правилом.
  Например: 4n⁴ + 4n² + 1 = 4n⁴ + Θ(n²) = Θ(n⁴). Отметим, что такая интерпретация подразумевает выполнение соотношения 4n⁴ + 4n² + 1 = Θ(n⁴).

Приведенная интерпретация подразумевает выполнение соотношения:

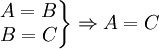$\left. \begin{matrix}A = B \\ B = C \end{matrix} \right\} \Rightarrow A = C$, где A, B, C — выражения, которые могут содержать асимптотические обозначения.

Примеры использования

• e^x = 1 + x + x²/2 + O(x³) при x → 0.
• n! = O((n/e)^n+1/2) при n → ∞.
• T(n) = (n + 1)² = O(n²) при n → ∞.

Доказательство:

Если положить n₀ = 1 и c = 4, то для n≥1 будет выполняться неравенство (n + 1)² < 4n². Отметим, что нельзя положить n₀ = 0, так как T(0) = 1 и, следовательно, это значение при любой константе c больше c0² = 0.

• Функция T(n) = 3n³ + 2n² при n → ∞ имеет степень роста O(n³). Чтобы это показать, надо положить n₀ = 0 и c = 5. Можно, конечно, сказать, что T(n) имеет порядок O(n⁴), но это более слабое утверждение, чем то, что T(n) имеет порядок роста O(n³).
• Докажем, что функция 3ⁿ при n → ∞ не может иметь порядок O(2ⁿ). Предположим, что существуют константы c и n₀ такие, что для всех n ≥ n₀ выполняется неравенство 3ⁿ ≤ c2ⁿ. Тогда c ≥ (3/2)ⁿ для всех n ≥ n₀. Но (3/2)ⁿ принимает любое, как угодно большое, значение при достаточно большом n, поэтому не существует такой константы c, которая могла бы мажорировать (3/2)ⁿ для всех n больших некоторого n₀.
• T(n) = n³ + 2n² есть Ω(n³) при n → ∞. Для проверки достаточно положить c = 1. Тогда T(n) > cn³ для n = 0,1,....

История

Обозначение «„O“ большое» введено немецким математиком Паулем Бахманом (Paul Gustav Heinrich Bachmann) во втором томе его книги «Analytische Zahlentheorie» (Аналитическая теория чисел), вышедшем в 1894 году. Обозначение «„о“ малое» впервые использовано другим немецким математиком, Эдмундом Ландау (Edmund Georg Hermann Landau) в 1909 году; с работами последнего связана и популяризация обоих обозначений, в связи с чем их также называют символами Ландау.

См. также

• Бесконечно малая величина

Литература

• Д. Грин, Д. Кнут. Математические методы анализа алгоритмов : Пер. с англ. М.: Мир, 1987. — 120 с.
• Дж. Макконелл, Основы современных алгоритмов, Изд. 2 доп., М.: «Техносфера», 2004, 368 с ISBN 5-94836-005-9
• Джон Э. Сэвидж, Сложность вычислений, М.: «Факториал», 1998, 368 с ISBN 5-88688-039-9
• В. Н. Крупский, Введение в сложность вычислений, М.: «Факториал Пресс», 2006, 128 с ISBN 5-88688-083-6
• Herbert S. Wilf, Algorithms and Complexity, http://www.math.upenn.edu/~wilf/AlgComp3.html
• Кормен, Томас Х.; Лейзерсон, Чарльз И.; Ривест, Рональд Л.; Штайн, Клифорд Глава 3. Рост функций // Алгоритмы: построение и анализ, 2-е издание = Introduction to Algorithms second edition. — М.: «Вильямс», 2005. — С. 230 - 234. — ISBN 5-8459-0857-4