Несобственные интегралы — обобщение классического понятия интеграла на случай неограниченных функций и функций, заданных на бесконечном промежутке интегрирования (см. Интеграл). Определённый интеграл как предел интегральных сумм Римана может существовать (иметь… … Большая советская энциклопедия
Расходящиеся интегралы — интегралы с бесконечными пределами, а также с неограниченной подынтегральной функцией, равные бесконечности или же не имеющие определённого конечного значения. Например, интеграл Несобственные интегралы, Интеграл, Суммирование… … Большая советская энциклопедия
Френеля интегралы — интегралы вида и введённые О. Ж. Френелем (См. Френель) при решении задач дифракции света (См. Дифракция света). Несобственные Ф. и. равны S (∞) = С (∞) = 1/2. Таблицы Ф. и. приводятся во многих… … Большая советская энциклопедия
Несобственный интеграл — Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий: Предел a или b (или оба предела) являются бесконечными; Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].… … Википедия
Интегральное исчисление — раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. И. и. тесно связано с дифференциальным исчислением (См. Дифференциальное исчисление) и составляет вместе с ним одну из основных частей… … Большая советская энциклопедия
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — часть математики, в к рой функции и их обобщения изучаются методом пределов. Понятие предела тесно связано с понятием бесконечно малой величины, поэтому можно также сказать, что М. а. изучает функции и их обобщения методом бесконечно малых.… … Математическая энциклопедия
Интеграл — (от лат. integer целый) одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости… … Большая советская энциклопедия
Фурье интеграл — формула для разложения непериодической функции на гармонические компоненты, частоты которых пробегают непрерывную совокупность значений. Если функция f (x) удовлетворяет на каждом конечном отрезке условию Дирихле (см. Фурье ряд) и если… … Большая советская энциклопедия
Сингулярный интеграл — 1) одно из средств представления функций; под С. и. понимают интеграл вида , который при n → ∞ сходится (при тех или иных ограничениях на функцию f) к порождающей его функции f (х); функция Kn (x, t) называется… … Большая советская энциклопедия
Сходимость — математическое понятие, означающее, что некоторая переменная величина имеет Предел. В этом смысле говорят о С. последовательности, С. ряда, С. бесконечного произведения, С. непрерывной дроби, С. интеграла и т. д. Понятие С. возникает,… … Большая советская энциклопедия
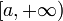 и
и 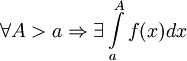 . Тогда:
. Тогда: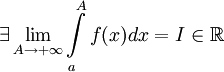 , то используется обозначение
, то используется обозначение 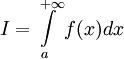 и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае 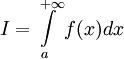 называется сходящимся.
называется сходящимся.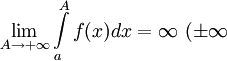 или
или 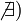 , то обозначается
, то обозначается 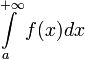 В этом случае интеграл называется расходящимся к
В этом случае интеграл называется расходящимся к 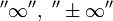 , или просто расходящимся.
, или просто расходящимся.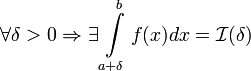 . Тогда:
. Тогда: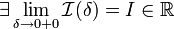 , то используется обозначение
, то используется обозначение 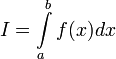 и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.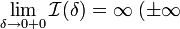 или
или 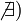 , то обозначение сохраняется, а
, то обозначение сохраняется, а 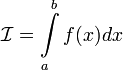 называется расходящимся к
называется расходящимся к 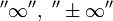 , или просто расходящимся.
, или просто расходящимся.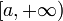 и
и 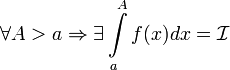 .
.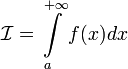 сходится
сходится 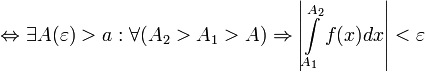
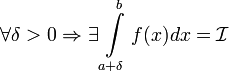 .
.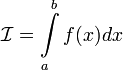 сходится
сходится 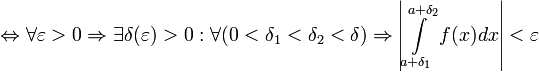
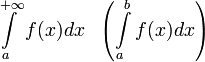 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если 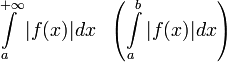 сходится.
сходится.