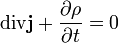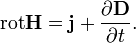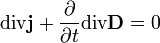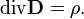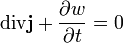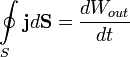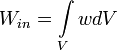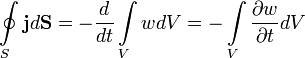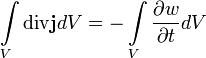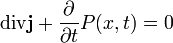Неразрывности уравнение

Ниже приведены примеры уравнений непрерывности, которые выражают одинаковую идею непрерывного изменения некоторой величины. Уравнения непрерывности — (сильная) локальная форма законов сохранения.

Электромагнетизм

В электродинамике уравнение непрерывности выводится из уравнений Максвелла. Оно утверждает, что дивергенция плотности тока равна изменению плотности заряда со знаком минус,

$\operatorname{div}\mathbf{j} + {\partial \rho \over \partial t} = 0$

Вывод

Закон Ампера гласит

$\operatorname{rot}\mathbf{H} = \mathbf{j} + {\partial \mathbf{D} \over \partial t}.$

Взяв дивергенцию от обоих частей выражения, получим

$\operatorname{div}\operatorname{rot}\mathbf{H}=\operatorname{div}\mathbf{j}+\frac{\partial }{\partial t}\operatorname{div}\mathbf{D}$,

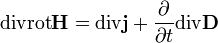но дивергенция ротора равняется нулю, таким образом

$\operatorname{div}\mathbf{j}+\frac{\partial }{\partial t}\operatorname{div}\mathbf{D}=0$

По теореме Гаусса

$\operatorname{div}\mathbf{D} = \rho.\,$

Подставляя это выражение в предыдущее уравнение, получаем искомое уравнение непрерывности.

Интерпретация

Плотность тока — это движение зарядов. Уравнение непрерывности гласит, что если заряд уходит из дифференциального объёма (то есть дивергенция плотности тока положительна), тогда количество заряда внутри объёма уменьшается. В этом случае скорость изменения плотности заряда отрицательна.

Теория волн

В теории волн уравнение непрерывности выражает собой закон сохранения энергии в элементарном объеме, в котором распространяются волны любой природы. Его дифференциальная форма

$\operatorname{div}\mathbf{j}+\frac{\partial w}{\partial t}=0$

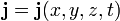где $\mathbf{j}=\mathbf{j}(x,y,z,t)$ — вектор плотности потока энергии в точке с координатами 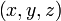$\left(x, y, z\right)$ в момент времени 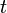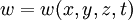$\,t$, $\,w=w(x,y,z,t)$ — плотность энергии.

Вывод

По определению, вектор плотности потока энергии — это вектор, модуль которого равен энергии, переносимой через единичную площадку, перпендикулярную направлению переноса энергии, за единицу времени, т.е. 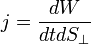$j=\frac{dW}{dtdS_{\bot }}$, а направление его совпадает с направлением переноса энергии. Тогда энергия, вытекающая в единицу времени из некоторого макроскопического объема V,

$\oint\limits_{S}{\mathbf{j}d\mathbf{S}}=\frac{dW_{out}}{dt}$

По закону сохранения энергии 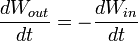$\frac{dW_{out}}{dt}=-\frac{dW_{in}}{dt}$, где W_in — энергия, находящаяся в объеме V. По определению, плотность энергии — энегрия единицы объема, тогда полная энегрия, заключенная в данном объеме, равна

$W_{in}=\int\limits_{V}{wdV}$

Тогда выражение для потока энергии примет вид

$\oint\limits_{S}{\mathbf{j}d\mathbf{S}}=-\frac{d}{dt}\int\limits_{V}{wdV}=-\int\limits_{V}{\frac{\partial w}{\partial t}dV}$

Применяя формулу Гаусса-Остроградского к левой части выражения, получим

$\int\limits_{V}{\operatorname{div}\mathbf{j}dV}=-\int\limits_{V}{\frac{\partial w}{\partial t}dV}$

В силу произвольности выбранного объема, заключаем что подынтегральные выражения равны, откуда и получаем дифференциальную форму уравнения непрерывности.

Гидродинамика

В гидродинамике уравнение непрерывности, иногда называемое уравнением неразрывности, выражает собой закон сохранения массы в элементарном объеме, то есть непрерывность потока жидкости или газа. Его дифференциальная форма

$\frac{\partial \rho }{\partial t}+\operatorname{div}\rho \mathbf{v}=\frac{\partial \rho }{\partial t}+\rho \operatorname{div}\,\mathbf{v}+\mathbf{v}\operatorname{grad}\rho =0$,

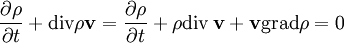где 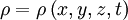$\rho = \rho\left(x,y,z,t\right)$ — плотность жидкости (или газа), 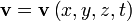$\mathbf{v}=\mathbf{v}\left( x,y,z,t \right)$ — вектор скорости жидкости (или газа) в точке с координатами 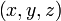$\left(x, y, z\right)$ в момент времени $\,t$.

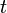Вектор 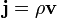$\mathbf{j}=\rho \mathbf{v}$ называют плотностью потока жидкости. Его направление совпадает с направлением течения жидкости, а абсолютная величина определяет количество вещества, протекающего в единицу времени через единицу площади, расположенную перпендикулярно вектору скорости.

Для несжимаемых жидкостей 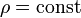$\,\rho = \operatorname{const}$. Поэтому уравнение принимает вид

$\operatorname{div}\,\mathbf{v}=0$,

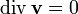из чего следует соленоидальность поля скорости.

Квантовая механика

В нерелятивистской квантовой механике сохранение вероятности также приводит к уравнению непрерывности. Пусть P(x, t) — плотность вероятности, тогда уравнение запишется в виде

$\operatorname{div}\mathbf{j}+\frac{\partial }{\partial t}P(x,t)=0$

где j — ток вероятности.