Модель Кронига-Пенни

В квантовой механике, частица в одномерном периодическом потенциале — это идеализированная задача, которая может быть решена точно (при некоторых специального вида потенциалах), без упрощений. Предполагается, что потенциал бесконечен и периодичен, то есть обладает трансляционной симметрией, что, вообще говоря, не выполняется для реальных кристаллов, и всегда существует как минимум один дефект — поверхность (это приводит к другой задаче о поверхностных состояниях или таммовских уровнях).

Постановка задачи

Рассмотрим одномерную решётку положительных ионов, расстояние между которыми 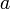$\! a$. Потенциал в этом случае будет выглядеть подобно этому:

Уравнение Шрёдингера в нашем случае:

$-\frac{\hbar^2}{2m}\frac{\partial^2 \psi (x)}{\partial x^2} + V_a(x) \psi (x) = E \psi (x)$

с периодическим потенциалом V_a(x) = V_a(x + a). Общий вид решения уравнения Шрёдингера с периодическим потенциалом, согласно теореме Блоха —

$\psi (x) = e^{ikx} u(x), \;$

где u(x) — некоторая периодическая функция:

u(x + a) = u(x).

k называют квазиимпульсом, по аналогии с волновой функцией e^ikx для частицы с определённым импульсом k.

Как видно, вся волновая функция определяется величиной k и любым участком функции длиной a.

При приближении к краям решётки появляется проблема граничных условий. Удобно представить решётку кольцом некоторой длины L >> a. Тогда вместо двух граничных условий у нас всего одно граничное условие:

$\psi (0)=\psi (L)\,$

Если N — число ионов в решётке, то aN = L. Подставляя волновую функцию в граничное условие, получаем квантование для k:

$\psi (0) = e^{ik \cdot 0} u(0) = e^{ikL} u(L) = \psi (L)\,$

$u(0) = e^{ikL} u(N a) \rightarrow e^{ikL} = 1\,$

$\Rightarrow kL=2\pi n \rightarrow k= {2\pi \over L} n \qquad \left( n=0, \pm 1, \pm 2, ..., \pm {N \over 2} \right).\,$

Модель Кронига — Пенни

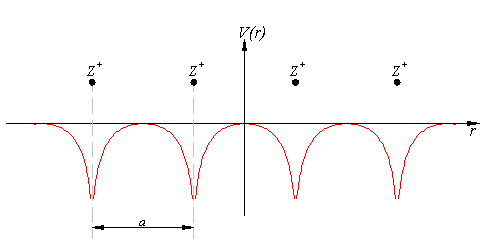
Для упрощения задачи потенциал приближают прямоугольным:

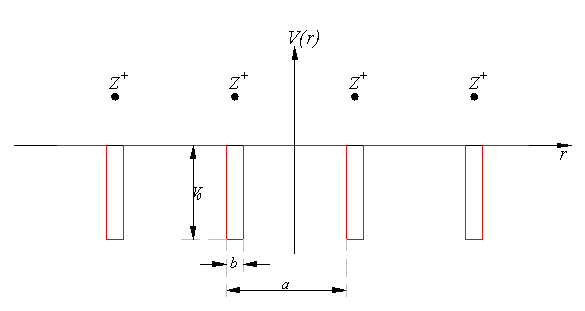
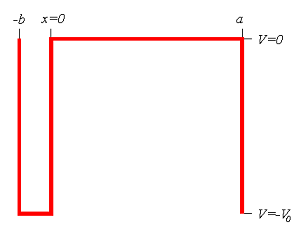
Используя теорему Блоха мы найдём волновую функцию во всём пространстве, но сначала надо найти решение для одного периода, и сделать его гладким на краях, то есть «сшить» значения соседних функций и их производных. Рассмотрим один период потенциала:

У нас есть две независимых области для которых мы найдём решения:

$0<x<a-b : {-\hbar^2 \over 2m} \psi_{xx} = E \psi$

$\Rightarrow \psi = A e^{i \alpha x} + A' e^{-i \alpha x} \quad \left( \alpha^2 = {2mE \over \hbar^2} \right)$

$-b<x<0 : {-\hbar^2 \over 2m} \psi_{xx} = (E+V_0)\psi$

$\Rightarrow \psi = B e^{i \beta x} + B' e^{-i \beta x} \quad \left( \beta^2 = {2m(E+V_0) \over \hbar^2} \right)$

Для нахождения u(x) в каждой области нужно проделать следующие преобразования:

$\psi(0<x<a-b) = A e^{i \alpha x} + A' e^{-i \alpha x} = e^{ikx} \cdot \left( A e^{i (\alpha-k) x} + A' e^{-i (\alpha+k) x} \right)$

$\Rightarrow u(0<x<a-b)=A e^{i (\alpha-k) x} + A' e^{-i (\alpha+k) x}$

Аналогично получим

$u( -b<x<0)=B e^{ i (\beta - k) x} + B' e^{ - i ( \beta + k ) x} \;$

Чтобы найти полное решение нам надо убедиться в гладкости искомой функции на границах:

$\psi(0^{-})=\psi(0^{+}) \quad \psi'(0^{-})=\psi'(0^{+})$

и периодичности u(x) и u'(x)

$u(-b)=u(a-b) \quad u'(-b)=u'(a-b).\,$

Эти условия дают следующую матрицу:

$\begin{pmatrix} 1 & 1 & -1 & -1 \\ \alpha & -\alpha & -\beta & \beta \\ e^{i(\alpha-k)(a-b)} & e^{-i(\alpha+k)(a-b)} & -e^{-i(\beta-k)b} & -e^{i(\beta+k)b} \\ (\alpha-k)e^{i(\alpha-k)(a-b)} & (\alpha+k)e^{-i(\alpha+k)(a-b)} & -(\beta-k)e^{-i(\beta-k)b} & (\beta+k)e^{i(\beta+k)b} \end{pmatrix} \begin{pmatrix} A \\ A' \\ B \\ B' \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}$

Для существования нетривиального решения необходимо зануление детерминанта этой матрицы. После некоторых преобразований получаем:

$\cos(k a) = \cos(\beta b) \cos[\alpha(a-b)]-{\alpha^2+\beta^2 \over 2\alpha \beta} \sin(\beta b) \sin[\alpha(a-b)]. \qquad ( * )$

Для дальнейшего упрощения мы выполним следующие упрощения, смысл которых заключается к переходу к дельта-образным потенциалам (дираковская гребёнка) :

$b \rightarrow 0 \ ; \ V_0 \rightarrow \infty \ ; \ V_0 b = \mathrm{constant}$

$\Rightarrow \beta b \rightarrow 0 \ ; \ \beta^2 b = \mathrm{constant} \ ; \ \alpha^2 b \rightarrow 0 \ ; \ \sin(\beta b) \rightarrow \beta b \ ; \ \cos(\beta b) \rightarrow 1$

Тогда конечный ответ будет:

$\cos(k a) = \cos(\alpha a)-P{\sin(\alpha a) \over \alpha a} \qquad \left( P={\beta^2 a b \over 2} \right)$

Программный код

Код для Maple

Следующий программный код написан на языке ( * ).

  restart;
  with(plots):
  with(stats[statplots]):
  eq:=cos(k*a)=cos(beta*b)*cos(alpha*(a-b)) - (alpha^2+beta^2)/(2*alpha*beta)*sin(beta*b)*sin(alpha*(a-b));
  alpha:=sqrt(8*Pi^2*m*(E)*e/h^2):
  beta:=sqrt(4*Pi^2*m*(E+V)*e/h^2):
  e:=1.6*1e-19:
  a:=0.54310*1e-9:
  m:=0.19*9.1*1e-31:
  b:=1/5*a:
  h:=6.6*1e-34:
  k(E,V):=arccos(rhs(evalf(eq)));

  #График
  p:=plot({subs(V=10,k(E,V)),subs(V=10,-k(E,V))},E=-5..50,labels=[ka, E],color=blue):
  xyexchange(p);

  #Анимация, зависимость от глубины ямы
  p:=animate( plot, [{k(E,V),-k(E,V)},E=-10..50, color=blue,labels=[ka, E]], V=0..30 ):
  xyexchange(p);

На рисунках представлены графические решения уравнения ( * ).

Линии отвечают разрешённым значениям энергии. Существуют области по энергии, где ни при каких значениях волнового вектора невозможно существование электрона. Линии отвечают разрешённым значениям энергии. Показано движение закона дисперсии в зависимости от глубины потенциальной ямы. На правом рисунке видно, как при некотором значении потенциальной энергии возможно образование одномерного безщелевого полупроводника.

Код для Scilab

Линии по прежнему отвечают разрешённым значениям энергии. Синим изображено решение для модели Кронига-Пенни, красным - гребёнки Дирака при тех же значениях V₀b

Код ниже является фактически переводом предшествующей программы на язык

clear all
 
global Pi e a m b h
 
Pi = 3.1415926;
 
step = 0.1;
 
e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;
 
function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(4*Pi^2*m*(E+V)*e/h^2);
endfunction
 
function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) / (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
endfunction
 
function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) / 2 .* sin(alpha*a) / (alpha * a));
endfunction
 
E = [0 : step: 50];
 
k = kronigpenney(10, E);
plot(k, E, 'b'); plot(-k, E, 'b');
 
k = dirac(10, E);
plot(k, E, 'r'); plot(-k, E, 'r');

Ссылки

• Задачи по квантовой механике. Часть 1. Галицкий, Карнаков, Коган.
• 1-D periodic potential applet
• Energy band formation