- КРОНИГА - ПЕННИ МОДЕЛЬ
- КРОНИГА - ПЕННИ МОДЕЛЬ
-
- одномерная, точно решаемая модель движения электронов в периодич. поле, иллюстрирующая природу возникновения энергетич. зон в кристалле (см. Зонная теория). Предложена Р. Кронигом (R. Kronig) и У. Дж. Пенни (W.G. Penney) в 1931. В К.-П. м. потенциал V(x), создавае-
мый кристаллич. решёткой, аппроксимируется периодич. последовательностью прямоугольных потенц. ям глубиной V0 и шириной а, разделённых потенц. барьерами шириной Ь, так что постоянная решётки равна а+Ь (рис. 1). Решение ур-ния Шрёдингера с потенциалом V(x )имеет вид плоской волны, модулированной с периодом решётки:
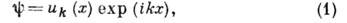
где uk(x )-периодич. ф-ция с периодом а+Ь (см. Блоховские электроны). Из условия непрерывности ф-ции и k (х )и её производной на границах ям ( х=0и
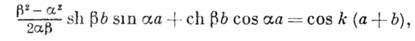 (2)
(2)
где
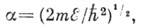
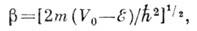 т- масса электрона.
т- масса электрона.
Ур-ние (2) упрощается, когда V(х) - периодич. последовательность дельта-функций (для этого нужно перейти к пределу
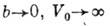 так, чтобы произведение V0 Ь оставалось постоянным):
так, чтобы произведение V0 Ь оставалось постоянным):
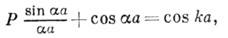 (3)
(3)
где
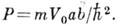
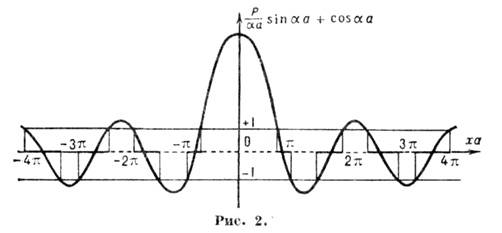
Т. <к. cos ka может принимать значения только в интервале от -1 до +1, величина
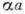 при заданном Р может принимать лишь те значения, при к-рых левая часть (3) не выходит из этого интервала (рис. 2). Границам допустимых значений
при заданном Р может принимать лишь те значения, при к-рых левая часть (3) не выходит из этого интервала (рис. 2). Границам допустимых значений 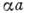 соответствуют значения k=
соответствуют значения k=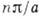 (n=1,2,...). Отсюда следует, что энергия
(n=1,2,...). Отсюда следует, что энергия 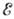 электрона не может принимать любое значение; энергетич. спектр разбивается на ряд полос энергии (разрешённых зон), разделённых запрещёнными зонами, ширина к-рых при больших п порядка
электрона не может принимать любое значение; энергетич. спектр разбивается на ряд полос энергии (разрешённых зон), разделённых запрещёнными зонами, ширина к-рых при больших п порядка
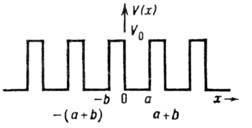
Pиc. 1. Одномерный периодический потенциал V(х) в модели Кронига.
х=а )получается дисперсионное ур-ние, связывающее энергию
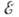 электрона с его волновым вектором k:
электрона с его волновым вектором k:При
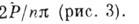
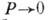 запрещённые области исчезают (электрон становится свободным); при Р-"оо разрешённые интервалы значений a а вырождаются в точки np и энергетич. спектр становится дискретным. Собств. значения энергии в этом случае
запрещённые области исчезают (электрон становится свободным); при Р-"оо разрешённые интервалы значений a а вырождаются в точки np и энергетич. спектр становится дискретным. Собств. значения энергии в этом случае 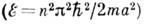 соответствуют электрону в бесконечно глубокой потенц. яме шириной
соответствуют электрону в бесконечно глубокой потенц. яме шириной 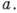 К. - П. м. позволяет вычислить также волновую ф-цию электрона.
К. - П. м. позволяет вычислить также волновую ф-цию электрона.
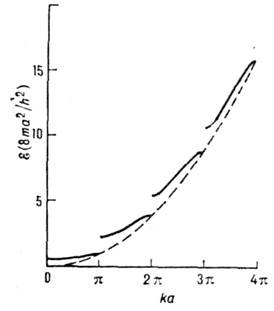
Рис. 3. Зависимость энергии от волнового числа для потенциала Кронига - Пенни при Р=
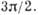
Лип.: Кrоnig R. de L., Penney W. G., Quantum mechanics of electrons in crystal lattices, "Proc. Roy. Soc. London", 1931, v. 130A, p. 499; Бете Г., 3оммерфельд А., Электронная теория металлов, пер. с нем., Л.- М., 1938; Киттель Ч., Введение в физику твердого тела, [пер. с англ.], 2 изд., М., 1963. д. М. Эпштепн.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
