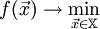Метод градиентного спуска

Градиентный спуск — метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.

Сходимость метода градиентного спуска зависит от отношения максимального и минимального собственных чисел матрицы Гессе в окрестности минимума (максимума). Чем больше это отношение, тем хуже сходимость метода.

Описание

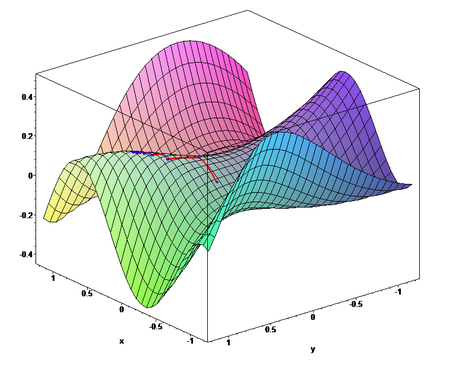
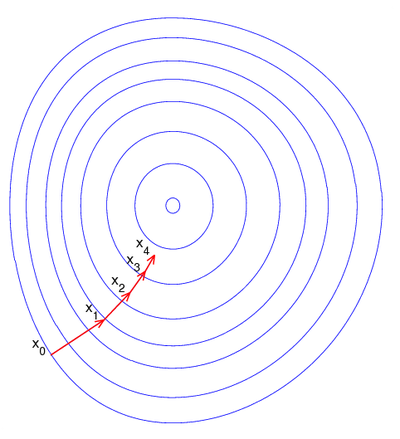Иллюстрация последовательных приближений к точке экстремума в направлении наискорейшего спуска (красн.) в случае дробного шага. Синим отмечены линии уровня.

Пусть целевая функция имеет вид:

$f(\vec{x}):\;\mathbb{X}\to\mathbb{R}$.

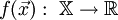И задача оптимизации задана следующим образом:

$f(\vec{x})\to\min_{\vec{x}\in\mathbb{X}}\!$

Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом $-\nabla F$:

$\overrightarrow{x}^{[j+1]}=\overrightarrow{x}^{[j]}-\lambda^{[j]}\nabla F(\overrightarrow{x}^{[j]}) \!$

где λ^[j] выбирается

• постоянной, в этом случае метод может расходиться;
• дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
• наискорейшим спуском: $\lambda^{[j]}=\mathrm{argmin}_{\lambda} \,F(\vec{x}^{[j]}-\lambda^{[j]}\nabla F(\vec{x}^{[j]})) \!$

Алгоритм

1. Задают начальное приближение и точность расчёта $\vec{x}^0, \quad \varepsilon$
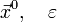
2. Рассчитывают $\overrightarrow{x}^{[j+1]}=\overrightarrow{x}^{[j]}-\lambda^{[j]}\nabla F(\overrightarrow{x}^{[j]}) \!$, где $\lambda^{[j]}=\mathrm{argmin}_{\lambda} \,F(\vec{x}^{[j]}-\lambda^{[j]}\nabla F(\vec{x}^{[j]})) \!$
3. Проверяют условие остановки:
   • Если $|\vec{x}^{[j+1]}-\vec{x}^{[j]}|>\varepsilon\!$, то j = j + 1 и переход к шагу 2.
   • Иначе $\vec{x}=\vec{x}^{[j+1]}\!$ и останов.

Пример

Применим градиентный метод к функции 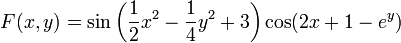$F(x,y)=\sin\left(\frac{1}{2} x^2 - \frac{1}{4} y^2 + 3 \right) \cos(2 x+1-e^y)$. Тогда последовательные приближения будут выглядеть так: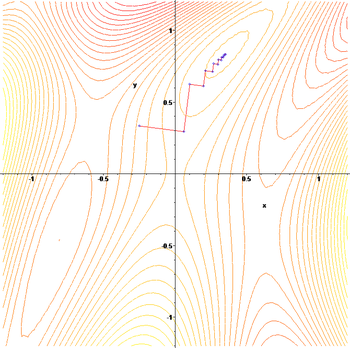

Упомянем, что метод наискорейшего спуска может иметь трудности в патологических случаях овражных функций, так, к примеру, в случае функции Розенброка.

Пример реализации

C++

#include <vector>
#include <iostream>
#include <Math.h>
#include <string>
#include <sstream>
#include <TCHAR.h>
 
using namespace std;
 
typedef vector<double> DataList;
 
void InitData();
void GradSearch(DataList &p, double sigma,double epsilon);
void QMin(DataList &de_dxi, DataList &p, double epsilon, double sigma);
void getDfDx(DataList &de_dxi, DataList &p);
string CreateResultString(DataList &pMin,double yMin);
double getFunc(DataList &p);
string stringify(double x);
 
DataList p1;
DataList p2;
DataList pMin;
DataList de_dxi;
 
double yMin;
double err;
double z0;
double h;
int N;
 
int j;
 
int main(int argc, _TCHAR* argv[])
{
	N = 2;
 
	InitData();
 
	DataList p;
	p.push_back(0.99);
	p.push_back(1.01);
        double sigma = 0.0000000001;
        double epsilon = 0.0000000001;
 
 
	GradSearch(p, sigma, epsilon);
 
	return 0;
}
 
void GradSearch(DataList &p, double sigma,double epsilon)
{
	int max = 60;
	h = 1;
	err = 1;
	int count = 0;
 
	while(count < max && (h>sigma ||err > epsilon))
	{
		getDfDx(de_dxi, p);
		QMin(de_dxi, p, epsilon, sigma);
 
		for(int i = 0; i<N; i++)
			p.at(i) = pMin.at(i);
 
		z0 = yMin;
		count = count + j + 1;
 
		string iterResult = CreateResultString(pMin, yMin);
 
		cout<<CreateResultString(pMin, yMin)<<endl;
	}
	cout<<endl<<"Минимум функции: "<<"-4*x + x*x - y - x*y + y*y"<<endl;
	cout<<CreateResultString(pMin, yMin)<<endl;
}
 
void QMin(DataList &de_dxi,DataList &p, double epsilon, double sigma)
{
	int cond = 0;
	int jmax = 60;
 
	z0 = getFunc(p);
 
	for(int i = 0; i<N; i++)
		p1.at(i) = p.at(i) + h * de_dxi.at(i);
 
	double y1 = getFunc(p1);
 
	for(int i = 0; i<N; i++)
		p2.at(i) = p.at(i) + 2 * h * de_dxi.at(i);
 
	double y2 = getFunc(p2);
 
	j = 0;
 
	while (j<jmax && cond == 0)
	{
		if (z0<=y1)
		{
			for(int i = 0; i<N; i++)
				p2.at(i) = p1.at(i);
 
			y2 = y1;
			h = h / 2;
 
			for(int i = 0; i<N; i++)
				p1.at(i) = p.at(i) + h * de_dxi.at(i);
 
			y1 = getFunc(p1);
		}
		else if (y2 < y1)
		{
			for(int i = 0; i<N; i++)
				p1.at(i) = p2.at(i);
 
			y1 = y2;
 
			h = h*2;
 
			for(int i = 0; i<N; i++)
				p2.at(i) = p.at(i) + 2 * h * de_dxi.at(i);
 
			y2 = getFunc(p2);
		}
		else
		{
			cond = -1;
		}
 
		j = j+1;
		if (h < sigma)
			cond = 1;
	}
 
	double hMin = (h/2)* (4 * y1 - 3* z0 - y2) / (2* y1 - z0 - y2);
 
	for (int i = 0; i< N; i++)
	{
		pMin.at(i) = p.at(i) + hMin * de_dxi.at(i);
	}
 
	yMin = getFunc(pMin);
 
	double h0 = fabs(hMin);
	double h1 = fabs(hMin - h);
	double h2 = fabs(hMin - 2* h);
 
	if (h0 < h)
		h = h0;
	if (h1 < h)
		h = h1;
	if (h2 < h)
		h = h2;
	if (h == 0)
		h = hMin;
	if (h < sigma)
		cond = 1;
	double e0 = fabs(z0 - yMin);
	double e1 = fabs(y1 - yMin);
	double e2 = fabs(y2 - yMin);
 
	if (e0 != 0 && e0 < err)
		err = e0;
	if (e1 != 0 && e1 < err)
		err = e1;
	if (e2 != 0 && e2 < err)
		err = e2;
	if (e0 == 0 && e1 == 0 && e2 == 0)
		err = 0;
	if (err < epsilon)
		cond = 2;
}
 
double getFunc(DataList &p)
{
	double x = p.at(0);
	double y = p.at(1);
 
	double result = -4 * x + x*x - y - x * y + y * y;
 
	return result;
}
 
void getDfDx(DataList & de_dxi, DataList &p)
{
	double x = p.at(0);
	double y = p.at(1);
 
 
	double dfDx = -4+2*x-y;
	double dfDy = -1-x+2*y;
 
	double norm = sqrt(dfDx*dfDx + dfDy*dfDy);
 
	dfDx = -dfDx/norm;
	dfDy = -dfDy/norm;
 
	de_dxi.at(0) = dfDx;
	de_dxi.at(1) = dfDy;
}
 
void InitData()
{
	for(int i = 0; i<N; i++)
	{
		p1.push_back(0);
 
		p2.push_back(0);
 
		pMin.push_back(0);
 
		de_dxi.push_back(0);
	}
}
 
string stringify(double x)
{
	ostringstream o;
	if (!(o << x))
		return 0;
	return o.str();
}
 
string CreateResultString(DataList &pMin,double yMin)
{
	string resultStr = "f[";
 
	for(int i = 0; i<N; i++)
	{
		if (i != 0)
			resultStr += ",";
		resultStr += stringify(pMin.at(i));
	}
 
	resultStr += "] = " + stringify(yMin);
 
	return resultStr;
}

Ссылки

• Mathematics Department at Cal State Fullerton
• Поиск глобального оптимума для задач оптимального проектирования систем или определения оптимальных законов управления.

Литература

1. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
2. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
3. Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
4. Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
5. Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
6. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.

См. также

Градиентные методы

• Метод покоординатного спуска
• Метод сопряжённых градиентов