- Метод грубой силы
-
Полный перебор (или метод «грубой силы» от англ. brute force) — метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от размерности пространства всех возможных решений задачи. Если пространство решений очень велико, то полный перебор может не дать результатов в течение нескольких лет или даже столетий.
Любая задача из класса NP может быть решена полным перебором. При этом, даже если вычисление целевой функции от каждого конкретного возможного решения задачи может быть осуществлена за полиномиальное время, в зависимости от количества всех возможных решений полный перебор может потребовать экспоненциального времени работы.
В криптографии на сложности полного перебора основывается оценка криптостойкости шифров. В частности, шифр считается криптостойким, если не существует метода «взлома» существенно более быстрого чем полный перебор всех ключей. Криптографические атаки, основанные на методе полного перебора, являются самыми универсальными, но и самыми долгими.
Содержание
Методы оптимизации полного перебора
Для увеличения скорости подбора ключа используется распараллеливание вычислений. Известно два направления распараллеливания.
- Во-первых, построение конвейера. Пусть алгоритм соотношения
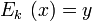 можно представить в виде цепочки простейших действий (операций):
можно представить в виде цепочки простейших действий (операций): 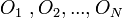 . Возьмем
. Возьмем 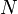 процессоров
процессоров 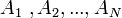 , зададим их порядок и положим, что
, зададим их порядок и положим, что 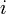 — ый процессор выполняет три одинаковые по времени операции:
— ый процессор выполняет три одинаковые по времени операции:
- приём данных от
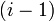 — го процессора;
— го процессора; - выполнение операции
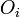 ;
; - передача данных следующему
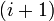 -му процессору.
-му процессору.
- Тогда конвейер из
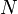 последовательно соединённых, параллельно и синхронно работающих процессоров работает со скоростью
последовательно соединённых, параллельно и синхронно работающих процессоров работает со скоростью 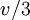 , где
, где 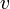 — скорость выполнения одной операции одним процессором.
— скорость выполнения одной операции одним процессором.
- приём данных от
- Второе направление распараллеливания состоит в том, что множество
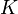 всех возможных ключей разбивается на непересекающиеся подмножества
всех возможных ключей разбивается на непересекающиеся подмножества 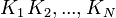 . Система из
. Система из 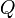 машин перебирает ключи так, что
машин перебирает ключи так, что 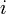 — ая машина осуществляет перебор ключей из множества
— ая машина осуществляет перебор ключей из множества 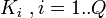 . Система прекращает работу, если одна из машин нашла ключ. Самой трудное — это разделение ключевого множества. Но если каждый процессор начнёт вычисление с какого-то произвольного ключа, то время нахождения увеличится, а схема значительно упростится. Среднее число шагов в этом случае составляет
. Система прекращает работу, если одна из машин нашла ключ. Самой трудное — это разделение ключевого множества. Но если каждый процессор начнёт вычисление с какого-то произвольного ключа, то время нахождения увеличится, а схема значительно упростится. Среднее число шагов в этом случае составляет 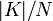 , где
, где 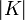 — число элементов во множестве ключей, а
— число элементов во множестве ключей, а 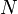 — число процессоров.
— число процессоров.
Реализация распараллеливания
Реализовать распараллеливание можно по-разному.
- Например, создать вирус для распространения программы-взломщика в глобальной сети. Он должен использовать свободное время процессора для перебора ключей. Рано или поздно один из зараженных компьютеров обнаружит искомый ключ и оповестит об этом злоумышленника.
- Существуют также более оригинальные идеи распараллеливания вычислений:
- «Китайская лотерея», создание «криптоаналитических» водорослей и животных.
- Китайская лотерея предполагает, что в каждый радиоприемник и телевизор встроена микросхема, запрограммированная на автоматическую проверку различных множеств ключей после получения по эфиру пары открытый текст/шифртекст.
- С использованием биотехнологий можно сделать криптоанализ ещё эффективнее. Можно создать существо, состоящее из клеток, умеющих тестировать ключи. Каким-то образом в клетки передаются пары открытый текст/шифртекст. Решения переносятся к органам речи специальными клетками, путешествующими по кровеносной системе существа. В доисторические времена средний динозавр состоял примерно из 1014 клеток (без микробов). Если каждая клетка может выполнять миллион шифрований в секунду, вскрытие 56-битового ключа займёт 7 * 10 − 4 сек, а 64-битового — не более 0,2 сек.
- Ещё один способ — создание водорослей, умеющих вскрывать криптографические алгоритмы методом полного перебора. Водоросли могут покрывать большие пространства, что теоретически позволит создать что-то вроде распределённого компьютера с огромным числом процессоров.
- «Китайская лотерея», создание «криптоаналитических» водорослей и животных.
Пример продолжительности подбора
Полное время раскрытия криптофайла для частного случая (100 000 паролей в секунду; 36 символов в алфавите (латинские буквы + цифры)).
Знаков Кол-во вариантов Время перебора 1 36 менее секунды 2 1296 менее секунды 3 46 656 менее секунды 4 1 679 616 17 секунд 5 60 466 176 10 минут, 5 секунд 6 2 176 782 336 6 часов, 2 минуты 7 78 364 164 096 9 дней, 2 часа, 16 минут, 26 секунд 8 2,821 109 9x1012 10 месяцев, 23 дня, 52 минуты, 37 секунд 9 1,015 599 5x1014 32 года, 3 месяца, 7 дней, 12 часов, 11 минут 10 3,656 158 4x1015 1161 год, 8 месяцев, 26 дней, 18 часов, 33 минуты, 40 секунд 11 1,316 217 0x1017 41 822 года, 7 месяцев, 20 дней, 6 часов, 44 минуты, 22 секунды 12 4,738 381 3x1018 1 505 614 лет, 11 месяцев, 30 дней, 1 час, 11 минут, 45 секунд (данные получены посредством программы Hacking Time Analizer)
Таким образом, пароли длиной менее 6 символов, в общем случае, не являются надежными.
При переборе с использованием технологии nVidia
См. также
- Во-первых, построение конвейера. Пусть алгоритм соотношения
Wikimedia Foundation. 2010.
