Метод вариации произвольных постоянных для построения решения линейного дифференциального уравнения

Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения

a_n(t)z⁽ⁿ⁾(t) + a_{n − 1}(t)z^{(n − 1)}(t) + ... + a₁(t)z'(t) + a₀(t)z(t) = f(t)

состоит в замене произвольных постоянных c_k в общем решении

z(t) = c₁z₁(t) + c₂z₂(t) + ... + c_nz_n(t)

соответствующего однородного уравнения

a_n(t)z⁽ⁿ⁾(t) + a_{n − 1}(t)z^{(n − 1)}(t) + ... + a₁(t)z'(t) + a₀(t)z(t) = 0

на вспомогательные функции c_k(t), производные которых удовлетворяют линейной алгебраической системе

$\left\{\begin{matrix} z_1(t)c_1^'(t) &+& z_2(t)c_2^'(t) &+& ... &+& z_n(t)c_n^'(t) &=& 0 \\ \vdots\\ z_1^{(n-2)}(t)c_1^'(t) &+& z_2^{(n-2)}(t)c_2^'(t) &+& ... &+& z_n^{(n-2)}(t)c_n^'(t) &=& 0 \\ a_n(z_1^{(n-1)}(t)c_1^'(t) &+& z_2^{(n-1)}(t)c_2^'(t) &+& ... &+& z_n^{(n-1)}(t)c_n^'(t))&=& f(t)\end{matrix}\right.\qquad(1)$

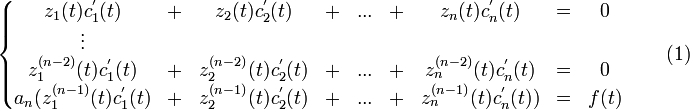
Определителем системы (1) служит вронскиан функций z₁,z₂,...,z_n, что обеспечивает её однозначную разрешимость относительно ${c_k^'}$.

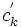Если 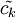$\tilde{c_k}$ — первообразные для 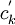$c_k^'$, взятые при фиксированных значениях постоянных интегрирования, то функция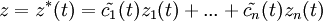

$z = z^*(t) = \tilde{c_1}(t)z_1(t) + ... + \tilde{c_n}(t)z_n(t)$

является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам.

Метод вариации постоянных называют также методом Лагранжа.

Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной форме

$\frac{d \bar{x}}{dt} = A(t)\bar{x} + \bar{f}(t), t\in I\qquad(1)$

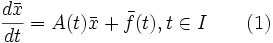
состоит в построении частного решения (1) в виде

$\bar{x} = \bar{x^*}(t) = Z(t)\bar{u}(t)$

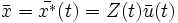
где Z(t) — базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция 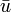$\bar{u}$, заменившая вектор произвольных постоянных, определена соотношением 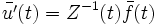$\bar{u'}(t) = Z^{-1}(t)\bar{f}(t)$. Искомое частное решение (с нулевыми начальными значениями при t = t₀ имеет вид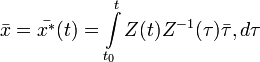

$\bar{x} = \bar{x^*}(t) = \int\limits_{t_0}^{t} Z(t)Z^{-1}(\tau)\bar{\tau}, d\tau$

Для системы с постоянными коэффициентами последнее выражение упрощается:

$\bar{x} = \bar{x^*}(t) = \int\limits_{t_0}^{t} Z(t - \tau) \bar{\tau}, d\tau$

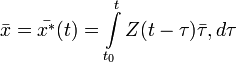
Матрица Z(t)Z ^{− 1}(τ) называется матрицей Коши оператора L = A(t).

Внешние ссылки

• exponenta.ru - Теоретическая справка c примерами