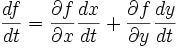Математика:Полная производная функции
Полезное
Смотреть что такое "Математика:Полная производная функции" в других словарях:
Исчисление — У этого термина существуют и другие значения, см. Исчисление (значения) … Википедия
Медицина — I Медицина Медицина система научных знаний и практической деятельности, целями которой являются укрепление и сохранение здоровья, продление жизни людей, предупреждение и лечение болезней человека. Для выполнения этих задач М. изучает строение и… … Медицинская энциклопедия
Дифференциал — (Differential) Определение дифферинциала, дифферинциал функции, блокировка дифферинциала Информация об определении дифферинциала, дифферинциал функции, блокировка дифферинциала Содержание Содержание математический Неформальное описание… … Энциклопедия инвестора
Лейбниц, Готфрид Вильгельм — Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия
Логарифм — График двоичного логарифма Логарифм числа … Википедия
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия
Интегральное исчисление — в сочинении Архимеда Об измерении длины окружности рассматривается вопрос об определении площади и длины окружности круга, а в трактате О шаре и цилиндре о поверхностях и объемах тел, ограниченных кривыми поверхностями; эти вопросы представляют… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Площадь — У этого термина существуют и другие значения, см. Площадь (значения). Площадь Размерность L² Единицы измерения СИ м² … Википедия
Информация — (Information) Информация это сведения о чем либо Понятие и виды информации, передача и обработка, поиск и хранение информации Содержание >>>>>>>>>>>> … Энциклопедия инвестора
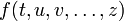 и ее аргументы зависят от времени:
и ее аргументы зависят от времени: 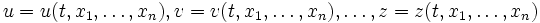 . Тогда
. Тогда 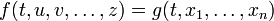 , где
, где 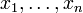 — параметры задающие траекторию. Полная производная функции f (в точке
— параметры задающие траекторию. Полная производная функции f (в точке 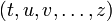 ) в таком случае равна частной производной g по времени (в соотвествующей точке
) в таком случае равна частной производной g по времени (в соотвествующей точке 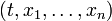 ) и может быть вычислена по формуле
) и может быть вычислена по формуле 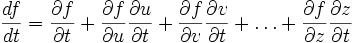 ,
,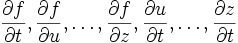 — частные производные. Следует отметить, что обозначение
— частные производные. Следует отметить, что обозначение 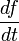 является условным и не имеет отношения к делению дифференциалов. Кроме того, полная производная функции зависит не только от самой функции, но и от траектории.
является условным и не имеет отношения к делению дифференциалов. Кроме того, полная производная функции зависит не только от самой функции, но и от траектории.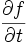 так как f сама по себе не зависит от t.
так как f сама по себе не зависит от t.