- Олимпиадные задачи
-
Олимпиадные задачи в математике — термин для обозначения круга задач, для решения которых обязательно требуется неожиданный и оригинальный подход.
Олимпиадные задачи получили своё название от популярных соревнований школьников и студентов, так называмых Математических олимпиад. Цель создания задач этой категории — воспитание в будущих математиках таких качеств как творческий подход, нетривиальное мышление и умение изучить проблему с разных сторон. Не случайно академик А. Н. Колмогоров в своей речи на открытии XII Всесоюзной Олимпиады школьников по математике сравнил работу математика с «чередой решения (порою больших и трудных) олимпиадных задач».
Внешняя простота олимпиадных задач — их условия и решения должны быть понятны любому школьнику — обманчива. Лучшие олимпиадные задачи затрагивают глубокие проблемы из самых разных областей математики. К сожалению, этой кажущейся простотой иногда пользовались не по назначению: на приёмных экзаменах с помощью таких задач отсеивали абитуриентов нежелательных национальностей . Неудивительно, что олимпиадные задачи из арсенала таких приёмных комиссий стали называть «гробами».
Олимпиадные задачи можно найти в Интернете, в периодических изданиях, а также в виде отдельных сборников. Они широко используются в работе математических кружков, заочных школ и для таких математических соревнований как олимпиады, турниры городов и математические бои.
Содержание
Примеры
Задача олимпиадного типа, известная со времён Евклида:
Доказать, что существует бесконечно много простых чисел.
Задача решается методом от противного. Предположив, что простых чисел конечное число N, рассматриваем число, следующее за их произведением (
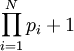 ). Очевидно, что оно не делится ни на одно из использованных в произведении простых чисел, давая в остатке 1. Значит, либо оно само простое, либо оно делится на простое число, не учтённое в нашем (предположительно полном) списке. В любом случае, простых чисел, по крайней мере, N+1. Противоречие с предположением о конечности.
). Очевидно, что оно не делится ни на одно из использованных в произведении простых чисел, давая в остатке 1. Значит, либо оно само простое, либо оно делится на простое число, не учтённое в нашем (предположительно полном) списке. В любом случае, простых чисел, по крайней мере, N+1. Противоречие с предположением о конечности. Типы задач
Несмотря на уникальность олимпиадных задач, можно всё-таки выделить несколько типичных идей, составляющих суть задач. Разумеется, по определению, такой список будет неполным.
См. также
- Категория:Олимпиадные задачи
Методы решения
Не существует единого метода решения олимпиадных задач. Напротив, количество методов постоянно пополняется. Некоторые задачи можно решить несколькими разными методами или комбинацией методов. Характерная особенность олимпиадных задач в том, что решение с виду несложной проблемы может потребовать применения методов, использующихся в серьёзных математических исследованиях. Ниже приводится (по определению) неполный список методов решения олимпиадных задач:
- Доказательство от противного.
- Принцип Дирихле.
- Решение методами другой науки (замена алгебраической задачи геометрической или физической и наоборот).
- Правило крайнего.
- Решение с конца.
- Поиск инварианта.
- Построение контрпримера.
- Математическая индукция.
- Рекурсия.
- Метод итераций.
- Подсчёт двумя способами.
- Метод аналогий.
- Провокационный метод.
- Вспомогательное построение.
- Переход в пространство большего числа измерений.
- Вспомогательная раскраска.
Большой вклад в популяризацию методов решения олимпиадных задач внесли публикации журнала «Квант», книги серий «Популярные лекции по математике», «Библиотека математического кружка» и другие книги, а также многочисленные веб-сайты, посвящённые олимпиадным задачам.
См. также
- Олимпиадные задачи по физике
Ссылки
Wikimedia Foundation. 2010.
