- ЭЙЛЕРА ФОРМУЛЫ
-
ф-лы, выражающие тригонометрич. функции переменного х через показат. функцию:
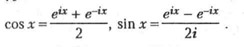
Установлены Л. Эйлером в 1743.
Естествознание. Энциклопедический словарь.
ф-лы, выражающие тригонометрич. функции переменного х через показат. функцию:
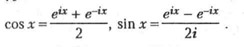
Установлены Л. Эйлером в 1743.
Естествознание. Энциклопедический словарь.
ЭЙЛЕРА ФОРМУЛЫ — формулы, выражающие тригонометрические функции переменного x через показательную функцию:Установлены Леонардом Эйлером … Большой Энциклопедический словарь
Эйлера формулы — формулы, выражающие тригонометрические функции переменного х через показательную функцию: , . Установлены Л. Эйлером. * * * ЭЙЛЕРА ФОРМУЛЫ ЭЙЛЕРА ФОРМУЛЫ, формулы, выражающие тригонометрические функции переменного x через показательную функцию:… … Энциклопедический словарь
ЭЙЛЕРА ФОРМУЛЫ — формулы, связывающие показательную и тригонометрические функции: справедливые при всех значениях комплексного переменного 2. В частности, при действительном z=x Э. ф. имеют вид: Эти формулы и были опубликованы Л. Эйлером [1]. Лит.:[1] Euler L.,… … Математическая энциклопедия
Эйлера формулы — в математике, важнейшие формулы, установленные Л. Эйлером. 1) Э. ф., связывающие тригонометрические функции с показательной (1743): eix = cos х + i sin х, , 2) Э. ф., дающая разложение функции sin х в… … Большая советская энциклопедия
Эйлера-Фурье формулы — формулы для вычисления коэффициентов разложения функции в тригонометрический ряд (ряд Фурье). Э. Ф. ф. названы по имени Л. Эйлера, давшего (1777) первый их вывод, и Ж. Фурье, систематически (начиная с 1811) пользовавшегося… … Большая советская энциклопедия
ЭЙЛЕРА - ФУРЬЕ ФОРМУЛЫ — формулы для коэффициентов Фурье ряда … Математическая энциклопедия
Эйлера числа — В комбинаторике числом Эйлера I рода из n по k, обозначаемым или E(n,k), называется количество перестановок порядка n с k подъёмами, то есть таких перестановок , что существует ровно k индексов j, для которых πj < πj + 1. Числа Эйлера I рода… … Википедия
ЭЙЛЕРА МЕТОД — простейший конечно разностный метод численного решения обыкновенных дифференциальных уравнений. Пусть дано дифференциальное уравнение с начальным условием y(x0) = y0. Выбирается достаточно малый шаг hпо оси х, строятся точки x;=x0+ih, i=0, 1, 2 … Математическая энциклопедия
ЭЙЛЕРА - МАКЛОРЕНА ФОРМУЛА — формула суммирования, связывающая частные суммы ряда с интегралом и производными его общего члена: где Бернулли числа, Rn остаточный член. С помощью Бернулли многочленов Bn(t), В n(0)=В п остаточный член записывается в виде: Для n=2sостаточный… … Математическая энциклопедия
Формула Эйлера — У этого термина существуют и другие значения, см. Список объектов, названных в честь Леонарда Эйлера#Формулы. Геометрический смысл формулы Эйлера Формула Эйлера на … Википедия