- ЭРЕНФEСТА ТЕОРЕМЫ
- ЭРЕНФEСТА ТЕОРЕМЫ
-
-теоремы, утверждающие, что ср. значения величин (координат, импульса, энергии), характеризующих движение частицы в квантовой механике, а также ср. значение силы, действующей на частицу, связаны между собой ур-ниями, аналогичными соответствующим ур-ниям классич. механики. Установлены П. Эрен-фестом (P. Ehrenfest, 1927) на основе сопоставления частице пакета волн де Бройля y(x, t )(см. Волновой пакет). В случае одной пространств. координаты ( х), учитывая, что |y( х, t)|2 есть плотность вероятности обнаружить частицу в нек-рой точке х, естественно вводится понятие "центра (тяжести)" волнового пакета как ср. значения координаты:
при этом считается, что y ( х, t )достаточно быстро спадает при
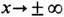и нормирована на единицу. Вычисление производной по времени от (1) с учётом Шрёдингера уравнения для одночастичного случая доказывает, что имеет место первая теорема Эренфеста: центр волнового пакета движется со скоростью, равной ср. импульсу частицы, отнесённому к её массе:
Отсюда, в частности, можно вывести явный вид самосопряжённых оператора импульса
и оператора координаты 
.
Вторая производная от (1) по времени приводит ко второй теореме Эренфеста: производная по времени от ср. импульса частицы равна ср. значению силы <Fx>= -<dU/dx>, приложенной к частице, т. <е.
Т. о., при условии, что размерами волнового пакета по сравнению с характерным масштабом изменения потенциала U(x )можно пренебречь, центр волнового пакета будет двигаться точно по законам классич. механики, записанным для ср. значений соответствующих физ. величин, т. е. соотношение между скоростью и импульсом частицы и 2-й закон Ньютона классич. механики выполняются в квантовой механике лишь для ср. значений физ. величин.
Для случая 3-мерных волновых пакетов Э. <т. (2) и (3) записываются соответственно в виде
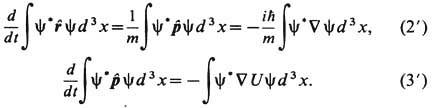
Пределы применимости Э. т. (т. е. справедливости классич. законов для квантовых средних) выводятся, в частности, из разложения ф-ции U(x )в окрестности "центра (тяжести)"
достаточно узкого пакета в ряд Тейлора и вычисления соответствующих квантовомеханич. средних. Если ограничиться первыми тремя членами разложения, то должны выполняться условия
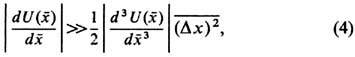
где
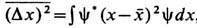, т. е. потенциал U должен достаточно плавно зависеть от 
. Кроме того, из сравнения выражений для кинетич. энергий классич. и квантовых частиц можно сделать вывод, что они сопоставимы лишь при достаточно больших импульсах, т. е. когда
из неопределённостей соотношения
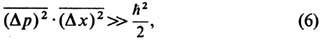
с учётом (4) и (5) выводится ещё одно условие, необходимое, чтобы квантовая частица подчинялась классич. законам:
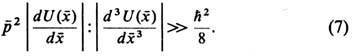
Выбор достаточно узких волновых пакетов приводит к большому разбросу по импульсам, что, в свою очередь, влечёт за собой быстрое "расплывание" пакетов (квадратичный по времени закон "расплывания"). Т. <о., волновой пакет можно сопоставить с частицей только для очень коротких временных промежутков. Поиск нерасплывающихся волновых пакетов или частицеподобных решений приводит к рассмотрению нелинейных обобщений ур-ний динамики (см. Солитон).
Лит.: Борисоглебский Л. А., Квантовая механика, 2 изд., Минск, 1988; Матвеев А. Н., Атомная физика, М., 1989; Рыбаков Ю. П., Терлецкий Я. П., Квантовая механика, М., 1991.
В. И. Санюк.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
