ХУНДА ПРАВИЛО

ХУНДА ПРАВИЛО

- правило для нахождения самых глубоких уровней энергии, соответствующих определённой э л е к т р о н н о й к о н ф и г у р а ц и и атома при н о р м а л ь-н о й с в я з и спиновых и орбитальных моментов образующих эти конфигурации электронов, когда уровни энергии характеризуются квантовыми числами S, L (см. Атом, Атомные спектры). В случае нормальной связи моментов (см. Связь векторная )при заданном квантовом числе S полного спинового момента атома и при заданном квантовом числе полного орбитального момента атома L получается с п е к т р а л ь н ы й т е р м 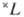с мультиплет-ностью 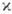=2S+1-совокупность уровней энергии с квантовыми числами J полного момента атома: J=L + S, L + S-1, ... , |L - S|. Расположение мультиплетных термов 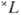определяется электростатич. взаимодействиями электронов (много большими при нормальной связи, чем магн. взаимодействия) и, как следует из эксперим. данных и подтверждается мн. квантовомеханич. расчётами, термы, соответствующие определённой конфигурации, лежат, как правило, тем глубже, чем больше S, а при данном S имеют тенденцию лежать тем глубже, чем больше L.

Согласно X. п., эмпирически установленному в 1925 Ф. Хундом (F. Hund), самый глубокий терм, соответствующий рассматриваемой электронной конфигурации, обладает наибольшим возможным значением S и наибольшим возможным для данного S значением L. Это правило всегда выполняется для н о р м а л ь н ы х э л е к т р о н н ы х к о н ф и г у р а ц и й, соответствующих наиб. прочной связи всех электронов и состоящих из эквивалентных электронов, и полностью подтверждается квантовомеханич. расчётами. Напр., для конфигурации р² получаются (при учёте Паули принципа )термы ¹S, ¹D,³ Р, а для конфигурации d²- термы ¹S, ¹D,¹G, ³P,³F; в первом случае самый глубокий терм, согласно X. п., ³ Р, во втором - ³F.

Для данного терма 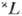уровни с различными J обладают разл. энергией-имеет место м у л ь т и п л е т н о е р а сщ е п л е н и е терма (при S<=L на =2S+1 составляющих и при S>L на 2L+1 составляющих), обусловленное магн. спин-орбитальным взаимодействием. Расположение уровней определяется приближённым п р а в и л о м и н т е р в ал о в, согласно к-рому расстояние между соседними уровнями с квантовыми числами J и J+1 пропорционально бoльшему квантовому числу; напр., для уровней ³ Р₀, ³P₁,³ Р₂. терма ³ Р расстояние ³ Р₂ -³ Р₁ вдвое больше расстояния ³ Р₁ -³ Р₀. При этом в случае конфигураций, состоящих из эквивалентных электронов, для оболочек, заполненных меньше чем наполовину (напр., р², d⁴, f⁵), получаются н о р м а л ь н ы е мультиплетные термы, для к-рых уровни лежат тем глубже, чем меньше J, а для оболочек, заполненных больше чем наполовину, получаются о б р ащ ё н н ы е мультиплетные термы, для к-рых уровни лежат тем глубже, чем больше J. Так, для нормального терма ³ Р конфигурации р² самый глубокий уровень ³ Р₀, а для обращённого терма дополнит. конфигурации р⁴-³ Р₂.

X. п. в сочетании с правилом нахождения наиб. глубокого уровня энергии для нормальных и обращённых мультиплетных термов (это правило иногда ошибочно наз. вторым X. п.) позволяет определить для нормальной конфигурации атома самый глубокий (основной) уровень энергии в тех случаях, когда в атоме частично заполнена наиб. слабо связанными электронами одна оболочка типа пр⁶, nd¹⁰ или nf¹⁴ (при наличии в атоме лишь полностью укомплектованных электронных оболочек осн. уровнем атома является уровень ¹S₀, а при наличии одного внеш. электрона ns - уровень ²S_l/2). Ниже приведены самые глубокие уровни энергии 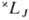для конфигурации эквивалентных электронов:

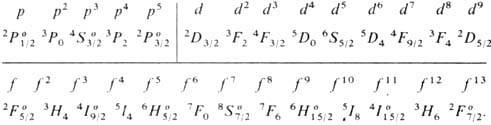
Отметим, что особенно глубоко (по сравнению с уровнями меньшей мультиплетности) лежат уровни ⁴S_3/2, ⁶S_5/2 и ⁸S_7/2 для оболочек p⁶, d¹⁰ и f¹⁴, заполненных как раз наполовину, т. е. для конфигураций р³, d⁵ и f⁷.

Лит.:Hund F., Linienspektren und periodisches System der Eie-mente, В., 1927; Ландау Л. Д., Лифшиц Е. М., Квантовая механика. Нерелятивистская теория, 4 изд., М., 1989; Ельяшевич М. А., Спектры редких земель, М., 1953; его же, Атомная и молекулярная спектроскопия, М., 1962; Собельман И. И., Введение в теорию атомных спектров, 2 изд., М., 1977. М. А. Ельяшевич.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.