- УСЛОВНАЯ ВЕРОЯТНОСТЬ
- УСЛОВНАЯ ВЕРОЯТНОСТЬ
-
с о б ы т и я А п р и у с л ов и и В- вероятность того, что произойдёт событие А при условии, что произошло событие В. Более подробно: пусть на вероятностном пространстве W (пространстве случаев или всех мыслимых исходов к.-н. испытания) задано распределение вероятностей {Р(А),
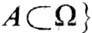 . Это означает, что каждому событию (множеству)
. Это означает, что каждому событию (множеству)  приписана его вероятность Р(A), причём так, что
приписана его вероятность Р(A), причём так, что

если два множества А и В не пересекаются (т. е. события А и В несовместны);
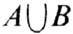 означает объединение множеств А и В, т. е. событие, включающее и А и В. Любое фиксир. множество В, такое, что Р(В)>0, можно рассматривать как новое вероятностное пространство (состоящее лишь из тех случаев, к-рые принадлежат В), и на нём можно задать новое вероятностное распределение:
означает объединение множеств А и В, т. е. событие, включающее и А и В. Любое фиксир. множество В, такое, что Р(В)>0, можно рассматривать как новое вероятностное пространство (состоящее лишь из тех случаев, к-рые принадлежат В), и на нём можно задать новое вероятностное распределение:
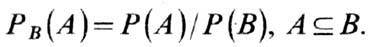
Вероятность Р B (А )наз. У. в. А при условии В[часто пишут Р(А|В)]. В случае, когда множество А целиком не лежит в В, полагают
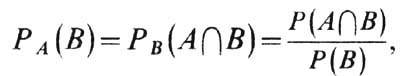
где
 -пересечение множеств А и В (т. е. событие, означающее, что А и В произошли одновременно).
-пересечение множеств А и В (т. е. событие, означающее, что А и В произошли одновременно).
В случае, когда
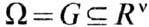 -область v -мерного пространства, v=l, 2, ...,
-область v -мерного пространства, v=l, 2, ...,  -гладкое подмногообразие в Rv, а распределение
-гладкое подмногообразие в Rv, а распределение 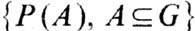 имеет плотность p(х), условное распределение Р(А|В )определяется ф-лой
имеет плотность p(х), условное распределение Р(А|В )определяется ф-лой
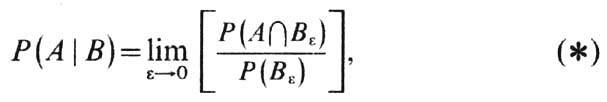
где Вe -e-окрестность В[предел (*) существует].
Лит.: Гнеденко Б. В., Курс теории вероятностей, 6 изд., М., 1988; Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., [3 изд.], т. 1, М., 1984. Р. А. Минлос.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
