- ТОНКИЕ ЖИДКИЕ ПЛЁНКИ
- ТОНКИЕ ЖИДКИЕ ПЛЁНКИ
-
(ТЖП) -плёнки жидкой фазы a, граничащие с одинаковыми b (симметричные ТЖП) или разными b и b' (несимметричные ТЖП) текучими (жидкими или газообразными) фазами и имеющие столь малую толщину, что взаимодействие их межфазных границ становится существенным. T. о., толщина ТЖП сопоставима с радиусом молекулярных корреляций в плёнке и граничащих фазах. Если фаза a - простая жидкость, то в обычных условиях толщина ТЖП составляет порядка неск. нм, однако достигает значит. размеров при приближении к критическому состоянию граничащих фаз, а также в том случае, когда ТЖП получены из растворов полимеров, мицеллярных растворов или жидких кристаллов.
К ТЖП по формальному признаку относят тонкие граничные слои жидкости на смачиваемых твёрдых поверхностях (см. Смачивание), жидкие прослойки между твёрдыми поверхностями, полимолекулярные адсорбц. слои поверхностно-активных веществ (ПАВ) на границе двух взаимно нерастворимых текучих фаз. К ТЖП относят также симметричные и несимметричные бислойные мембраны (в частности, бислойные липидные мембраны, образующие основу оболочек живых клеток; см. Клеточные структуры), состоящие из двух плотноупакованных слоев амфифильных молекул, гидрофобные (углеводородные) радикалы к-рых ориентированы внутрь мембраны, а гидрофильные- в сторону граничащих водных фаз.
Свойства практически важных дисперсных систем и природных объектов - эмульсий, пен, мицеллярных растворов, дисперсий коацерватных капель, везикул, биологических клеток и др.- определяются свойствами ТЖП, содержащихся в таких системах. Само существование этих систем зависит от взаимодействия между граничащими фазами в ТЖП и устойчивости ТЖП к прорыву.
Взаимодействие между дисперсными частицами, реализуемое через ТЖП, а также реологич. свойства ТЖП в большей степени влияют на энергетич. параметры, а также на вязкость, пластичность, эластичность, прочность дисперсных систем (напр., высококонцентрированных эмульсий, высокократных пен, живых клеток), чем реологич. свойства макроскопич. фаз, из к-рых образованы сами частицы.
Многочисл. технол. процессы, а также процессы и явления, происходящие в природе и живых организмах, сопровождаются образованием и разрушением ТЖП. В нек-рых случаях повышение устойчивости к прорыву (времени жизни) ТЖП является необходимым [напр., при длит. хранении высококонцентрированных эмульсий - топливных, пищевых, фармацевтич. и др., при транспортировании по трубопроводам нефтяных и битумных эмульсий, при движении эритроцитов по кровеносным сосудам, при пожаротушении (с помощью пен или смачивающих плёнок)]. В др. процессах, напротив, с помощью разл. физ.-хим. воздействий время жизни ТЖП должно быть уменьшено (напр., при слиянии биол. клеток, направленном транспорте по кровотоку нагруженных лекарственными средствами липо-сом в определ. органы, "прицельном" разрушении их оболочек и высвобождении лекарственных средств, при собирании плёнок нефти на поверхности водоёмов, образовании пен в биотехнол. реакторах, разрушении "соапстоков", образуемых в процессе рафинации растит. масел).
Формирование ТЖП может быть условно разбито на неск. характерных этапов, протекающих с разл. скоростью. При относительно большом расстоянии между сближающимися поверхностями текучих частиц (много большего радиуса действия поверхностных сил; рис. 1, а )вязкость, плотность и др. физ. свойства образующей жидкой "толстой" (не тонкой по определению) плёнки идентичны свойствам макроскопич. жидкой фазы а, из к-рой образована плёнка. Утоньшение такой жидкой плёнки описывается Навье - Стокса уравнениями гидродинамики с граничными условиями, учитывающими капиллярные эффекты (деформируемость межфазных поверхностей, поверхностные реологич. свойства адсорбц. слоев ПАВ и их диффузию, возникновение градиентов поверхностной плотности электрич. зарядов и величины адсорбции ПАВ, приводящие к градиенту межфазного натяжения, и др.).
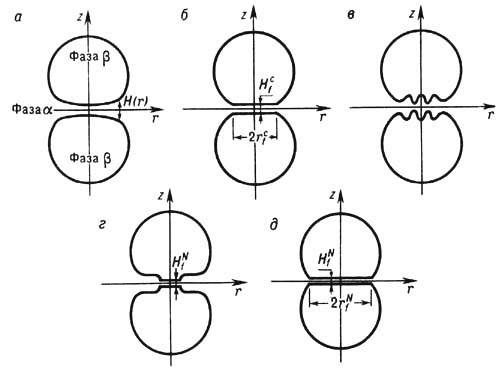
Рис. 1. Основные этапы формирования ТЖП при сближении двух капель или пузырьков: а- взаимное сближение межфазных поверхностей в условиях гидродинамического течения жидкой фазы a; б - образование относительно толстых (т. н. обычных чёрных) плёнок толщиной Hcf и радиусом rcf ; в- термические флуктуации толщины ТЖП, приводящие к их прорыву (коалесценции капель) или к образова нию чёоных пятен (т. н. ньютоновских чёрных плёнок) толщиной Р Nf( г), которые увеличиваются в разме ре, в результате чего ТЖП достигает pавновесного размера радиусом rNf (д).
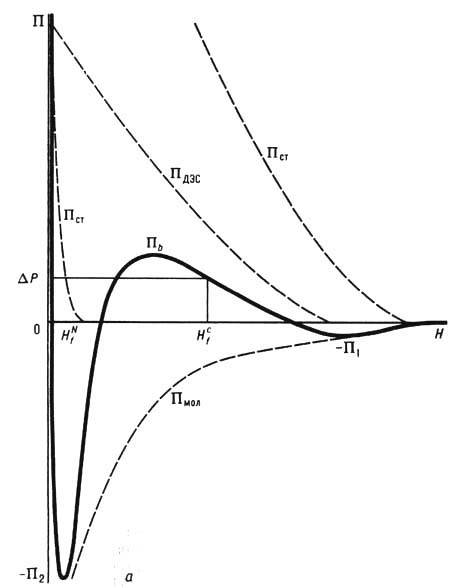
Рис. 2. Зависимость расклинивающего давления П (Hf) ТЖП от её толщины Hf; a -различные составляющие расклинивающего давления (пунктирные кривые) и результирующая изотерма расклинивающего давления (сплошная линия); б -тонкая плёнка воды, стабили зированная ионами ПАВ; в - ТЖП, стабилизированная адсорбционными слоями макромолекул.
При утоньшении жидкой плёнки до нек-рой толщины Hcf взаимодействие между межфазными поверхностями становится заметным (рис. 1, б), и описание кинетики утоньшения такой, уже тонкой по определению, плёнки требует учёта т. <н. р а с к л и н и в а ю щ е г о д а в л е н и я П (H), к-рое представляют в виде суммы независимых друг от друга вкладов поверхностных сил разл. природы: молекулярного притяжения П мол(H), ионно-электростатич. отталкивания между ДЭС - двойными электрич. слоями - П ДЭС(H) и контактного (стерического) взаимодействия между адсорбц. слоями ПАВ П ст( Н) [рис. 2; о термодинамич. определении П (H) см. ниже]:
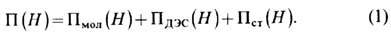
По соглашению, П( Н) считают положительным, если поверхности отталкиваются, и отрицательным, если они притягиваются.
Изотерму П мол (H) для ТЖП можно представить в виде
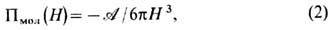
где A -т. н. постоянная Гамакера, учитывающая дисперс. взаимодействия между молекулами макроскопич. фаз (см. Межмолекулярное взаимодействие). Учёт эл.-магн. запаздывания для взаимодействующих молекул приводит к зависимости
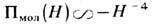
В макроскопич. теории межмолекулярного взаимодействия (E. M. Лифшиц, И. E. Дзялошинский, Л. П. Питаев-ский) П мол(H) рассчитывается путём суммирования энер-гетич. спектра эл.-магн. флуктуации в граничащих конденсированных средах в рамках квантовой статистики на основе спектральных характеристик конденсированных фаз.

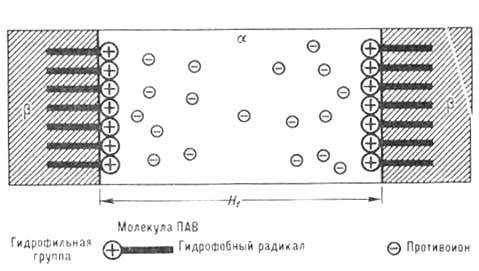
Для расчёта П дес(H) используются разл. аппроксимац. соотношения, выведенные на основе разл. моделей и механизмов образования ДЭС (рис. 1, б) и взаимодействия между ними. Сложности расчёта связаны в осн. с неопределённостью значения поверхностной плотности зарядов в процессе сближения межфазных поверхностей. В случае слабого перекрытия диффузных частей ДЭС П ДЭС( Н )обычно представляют в виде

где e0 -электрич. постоянная (диэлектрич. проницаемость вакуума); e-относительная диэлектрическая проницаемость среды ТЖП; е - заряд электрона; g=th(ey0/4kT); y0 - потенциал межфазной поверхности на границе с диффузной частью ДЭС; K=1/RD,
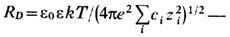 дебаевский радиус, ci и zi - концентрация и валентность i -го противоиона (рис. 2, б).
дебаевский радиус, ci и zi - концентрация и валентность i -го противоиона (рис. 2, б).
Непосредственный (стерический) контакт между двумя адсорбц. слоями ПАВ возникает на расстояниях порядка молекулярных размеров и приводит к т. <н. стерическому отталкиванию между межфазными поверхностями, описываемому изотермой:
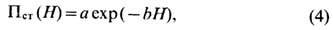
где а и b - коэффициенты (1/b имеет порядок длины молекулярной корреляции).
В общем случае результирующая изотерма расклинивающего давления П имеет дальний и ближний коагуляц. минимумы глубины П 1 и П 2 соответственно и коагуляц. барьер высоты П b (рис. 2, а). При достаточно высоком электрич. потенциале y0 межфазных поверхностей и низкой концентрации противоионов высота барьера П b может значительно превышать разность давлений
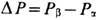 в фазах a и b и образуются т. <н. о б ы ч н ы е ч ё р н ы е п л ё н к и - ТЖП с относительно большой толщиной Hcf (Hcf - меньшe четверти длины видимого света; такие плёнки не отражают свет и потому в отражённом свете кажутся чёрными). При увеличении ci или снижении y0 высота барьера П b снижается и в обычных чёрных плёнках спонтанно возникают участки т. <н. н ь ю т о н о в с к и х ч ё р н ы х п л ё н о к толщиной Hcf, значительно меньшей Hcf, или происходит коалесценция текучих фаз b т. е. прорыв ТЖП (если макс. значение П ст<DP). Представления о влиянии концентрации и валентности противоионов на устойчивость обычных чёрных плёнок к переходу в ньютоновские чёрные плёнки или к прорыву ТЖП составляют основу теории ДЛФО, разработанной впервые Б. В. Дерягиным, Л. Д. Ландау, Э. Фервеем (E. J. W. Verwey) и Я. Овербе-ком (J. Th. G. Overbeek) для объяснения устойчивости гидрофобных золей к коагуляции.
в фазах a и b и образуются т. <н. о б ы ч н ы е ч ё р н ы е п л ё н к и - ТЖП с относительно большой толщиной Hcf (Hcf - меньшe четверти длины видимого света; такие плёнки не отражают свет и потому в отражённом свете кажутся чёрными). При увеличении ci или снижении y0 высота барьера П b снижается и в обычных чёрных плёнках спонтанно возникают участки т. <н. н ь ю т о н о в с к и х ч ё р н ы х п л ё н о к толщиной Hcf, значительно меньшей Hcf, или происходит коалесценция текучих фаз b т. е. прорыв ТЖП (если макс. значение П ст<DP). Представления о влиянии концентрации и валентности противоионов на устойчивость обычных чёрных плёнок к переходу в ньютоновские чёрные плёнки или к прорыву ТЖП составляют основу теории ДЛФО, разработанной впервые Б. В. Дерягиным, Л. Д. Ландау, Э. Фервеем (E. J. W. Verwey) и Я. Овербе-ком (J. Th. G. Overbeek) для объяснения устойчивости гидрофобных золей к коагуляции.
Составляющая П ст может явиться осн. фактором устойчивости ТЖП к прорыву в случае стабилизации их адсорбц. слоями макромолекул (напр., синтетич. полимерами или природными биополимерами-белками, полиса-хлридами). При достаточно высокой степени заполнения адсорбированными макромолекулами межфазных поверхностей для конформации макромолекул характерно наличие т. н. петель и хвостов (рис. 2, в), размеры к-рых порядка размеров макромолекулярных клубков в растворе и могут значительно превышать радиус действия молекулярных (ван-дер-ваальсовых) и электрич. сил в ТЖП. Расчёт П ст показывает, что профиль изотермы П ст (H )определяется в осн. взаимным отталкиванием "петель" и "хвостов", принадлежащих разл. адсорбц. слоям полимеров в ТЖП.
Разрушение (прорыв) ТЖП. Разрушение ТЖП (или скачкообразное утоньшение их до ньютоновских чёрных плёнок) происходит в момент достижения ими нек-рой "критич." толщины. При безбарьерном утоньшении обычной ТЖП время её жизни т определяется скоростью вытекания среды до момента прорыва. В случае существования коагуляц. барьера
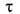 определяется в осн. высотой П b, а не гидродинамич. факторами.
определяется в осн. высотой П b, а не гидродинамич. факторами.
Существуют два подхода к объяснению влияния физ.-хим. факторов на устойчивость ТЖП к прорыву, основанные на разл. модельных представлениях ТЖП. Согласно первому подходу, применяемому для описания устойчивости обычных чёрных плёнок, жидкая плёнка представляется в виде непрерывной бездефектной жидкой среды, профиль к-рой в её "плоской" части возмущён термофлуктуац. волнами разл. длины и амплитуды (рис. 1, в). Прорыв такой плёнки происходит в результате возникновения кри-тич. термич. флуктуации её толщины, в результате чего локальное утоныпение плёнки становится столь значительным, что молекулярные силы притяжения могут приводить к необратимому утоньшению плёнки и её прорыву. Осн. допущение при этом заключается в условии выполнения неравенства 1/k >> H, где k - волновое число, что позволяет использовать ур-ния Навье - Стокса для одно-врем. описания вязкого ламинарного течения жидкости из плёнки при её утоньшении и волнового движения припо-верхностных слоев.
В рамках второго подхода, к-рый применяют для описания прорыва ньютоновских чёрных плёнок (в т. ч. бислой-ных мембран), ТЖП представляют в виде существенно "дефектной" среды, пронизанной термофлуктуационно возникающими и исчезающими "дырками" разл. радиусов r. Работу их образования представляют в виде
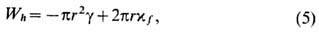
где g-натяжение плёнки (мембраны) - отнесённый к единице площади избыток свободной энергии системы (большого термодинамич. потенциала при постоянных темп-ре T и химических потенциалах компонентов
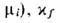 -линейное натяжение мембраны - отнесённый к единице длины периметра "дырки" избыток свободной энергии системы. При возникновении дефекта критич. размера происходит его неогранич. рост и прорыв ТЖП.
-линейное натяжение мембраны - отнесённый к единице длины периметра "дырки" избыток свободной энергии системы. При возникновении дефекта критич. размера происходит его неогранич. рост и прорыв ТЖП.
Термодинамическое описание ТЖП. Свойства ТЖП отличаются от свойств жидкой фазы a, и ТЖП не могут считаться фазой в точном термодинамич. смысле, поскольку они неоднородны по толщине и характеризуются значит. градиентами локальных плотностей соответствующих экстенсивных термодинамич. свойств - свободной энергии, энтропии, массы. Термодинамич. описание ТЖП основано на м е т о д е и з б ы т к о в Г и б б с а, позволяющем представить большой термодинамич. потенциал W системы, содержащей ТЖП, в виде суммы объёмной части WV, относящейся к макроскопич. фазам, и поверхностного избытка Wf, отнесённого к разделяющим поверхностям в плёнке.
В общем случае ТЖП образует вместе с граничащими с ней макроскопич. фазами многокомпонентную систему объёмом V, содержащую Ni молей каждого i -го компонента (i= 1, 2, ..., n; n - число компонентов в системе). В состоянии термодинамич. и механич. равновесия абс. темп-pa T и хим. потенциалы mi компонентов ТЖП равны во всех частях системы, а площадь А и толщина H ТЖП поддерживаются постоянными с помощью внеш. сил, к-рые уравновешивают давления Pa и Pb в фазах a и b и натяжение плёнки g. Если можно пренебречь силой тяжести, то фундам. термодинамич. ур-ние (см. Химическая термодинамика )для симметричной плоскопараллельной ТЖП имеет вид
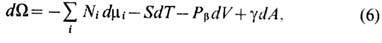
где S- энтропия системы. Поверхностный избыток Wf из ур-ния (6) можно выделить, используя два подхода: метод мембраны нулевой толщины и метод слоя конечной толщины.
М е т о д м е м б р а н ы н у л е в о й т о л щ и н ы заключается в условной замене открытой системы, содержащей ТЖП, на энергетически эквивалентную ей систему (референтную, по Гиббсу, систему, см. Поверхностные явления), в к-рой ТЖП заменена на разделяющую (по Гиббсу) поверхность, т. е. поверхность, хотя и имеющую нулевую толщину, однако характеризующуюся конечными значениями поверхностных плотностей свободной энергии, энтропии и массы. Весь объём V системы при этом считается заполненным фазой b: V=Vb Мембранный метод описания ТЖП используется в том случае, когда толщина плёнки не является экспериментально измеряемым параметром. Как и в случае свободных межфазных поверхностей, все экстенсивные параметры системы представляются в виде суммы объёмных частей, относящихся к фазе b, и поверхностных избытков, отнесённых к мембране f. В результате для случая плоскопараллельной ТЖП получаем два фундам. термодинамич. ур-ния — одно для референтной фазы
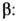

другое для мембраны f:
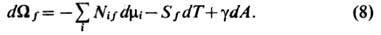
Из ур-ний (7) и (8) получается термодинамич. определение натяжения для плоской мембраны:
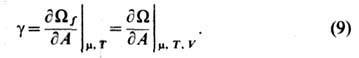
Применяя теорему Эйлера об однородных ф-циях, можно получить выражение для поверхностного избытка большого термодинамич. потенциала

а также Гиббса— Дюгема уравнение для мембраны
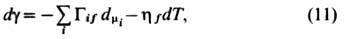
в к-ром
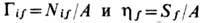 —отнесённые к единице поверхности мембраны избытки чисел молей i -ых компонентов (величины адсорбции i -компонентов относительно мембраны) и энтропии соответственно.
—отнесённые к единице поверхности мембраны избытки чисел молей i -ых компонентов (величины адсорбции i -компонентов относительно мембраны) и энтропии соответственно.
Ур-ние (9) составляет термодинамич. основу для вычисления натяжения мембраны
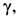 а также др. поверхностных избытков путём дифференцирования статистических сумм малого канонического (при постоянных Т и Ni) и большого канонического (при постоянных Т и
а также др. поверхностных избытков путём дифференцирования статистических сумм малого канонического (при постоянных Т и Ni) и большого канонического (при постоянных Т и  ) ансамблей (см. Гиббса распределения), выражаемых через потенциалы межмолекулярного взаимодействия и молекулярные ф-ции распределения. При этом учитываются энергия теплового движения атомов, молекул и ионов, энергия ван-дер-ваальсовых сил и сил эл.-статич. взаимодействия ионов и ионогенных групп в молекулах, а также сил бор-новского отталкивания и водородных связей.
) ансамблей (см. Гиббса распределения), выражаемых через потенциалы межмолекулярного взаимодействия и молекулярные ф-ции распределения. При этом учитываются энергия теплового движения атомов, молекул и ионов, энергия ван-дер-ваальсовых сил и сил эл.-статич. взаимодействия ионов и ионогенных групп в молекулах, а также сил бор-новского отталкивания и водородных связей.В рамках статистич. механики можно определить
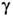 и прямым вычислением компонентов тензора давления, усреднённых по микроскопич. объёмам жидкостей среды путём суммирования возможных межмолекулярных взаимодействий. Основа метода—представления локальной (микроскопич.) термодинамики (или гидродинамич. приближения), согласно к-рым соотношения макроскопич. термодинамики выполняются в каждом сколь угодно малом микроскопич. элементе объёма анизотропной и неоднородной среды, какой является ТЖП. В отсутствие внеш. сил ср. значение обобщённого тензора давления должно удовлетворять условию равновесия:
и прямым вычислением компонентов тензора давления, усреднённых по микроскопич. объёмам жидкостей среды путём суммирования возможных межмолекулярных взаимодействий. Основа метода—представления локальной (микроскопич.) термодинамики (или гидродинамич. приближения), согласно к-рым соотношения макроскопич. термодинамики выполняются в каждом сколь угодно малом микроскопич. элементе объёма анизотропной и неоднородной среды, какой является ТЖП. В отсутствие внеш. сил ср. значение обобщённого тензора давления должно удовлетворять условию равновесия:
откуда следует, что нормальная к поверхности плоской ТЖП компонента тензора давления
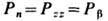 не зависит от координаты z (рис. 3, а), а тангенциальная компонента
не зависит от координаты z (рис. 3, а), а тангенциальная компонента 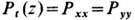 является сложной ф-цией координаты z (рис. 3, 6), причём в объёме фазы имеет место равенство
является сложной ф-цией координаты z (рис. 3, 6), причём в объёме фазы имеет место равенство 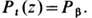
Для симметричной плоской ТЖП натяжение плёнки у вычисляется как поверхностный избыток объёмного тензора напряжений, т. е. удельной (отнесённой к единице длины) силе, действующей в плоскости мембраны перпендикулярно ограничивающей её линии:
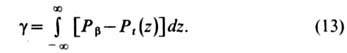
Для искривлённых ТЖП (в отличие от плоских) натяжение
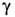 зависит от способа локализации разделяющей поверхности (мембраны). В частности, для сферич. ТЖП натяжение
зависит от способа локализации разделяющей поверхности (мембраны). В частности, для сферич. ТЖП натяжение 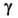 зависит от произвольно выбранного радиуса
зависит от произвольно выбранного радиуса 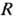 разделяющей поверхности:
разделяющей поверхности: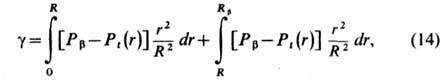
здесь
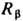 —радиус сферич. поверхности, проведённой в объёме фазы
—радиус сферич. поверхности, проведённой в объёме фазы 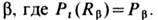
В общем случае искривлённой (несферической) мембраны её механич. состояние характеризуется отличными от нуля изгибающим В и скручивающим
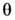 моментами, величины к-рых зависят от способа определения радиуса R мембраны. Фундам. ур-ние механич. равновесия такой мембраны (ур-ние Гиббса — Кельвина, или обобщённое ур-ние Лапласа) имеет вид
моментами, величины к-рых зависят от способа определения радиуса R мембраны. Фундам. ур-ние механич. равновесия такой мембраны (ур-ние Гиббса — Кельвина, или обобщённое ур-ние Лапласа) имеет вид 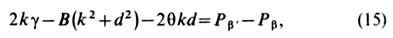
где
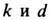 —средняя и дифференциальная (по Гиббсу) кривизны соответственно. Учёт механич. моментов становится существенным при термодинамич. описании ТЖП с низким и сверхнизким значениями
—средняя и дифференциальная (по Гиббсу) кривизны соответственно. Учёт механич. моментов становится существенным при термодинамич. описании ТЖП с низким и сверхнизким значениями 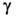 (напр., для бислойных липидных мембран, образующих оболочки клеточных структур и везикул). В случае сферич. ТЖП
(напр., для бислойных липидных мембран, образующих оболочки клеточных структур и везикул). В случае сферич. ТЖП 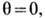 и если разделяющая поверхность выбрана т. о., чтобы
и если разделяющая поверхность выбрана т. о., чтобы 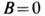 (т. н. поверхность натяжения радиуса
(т. н. поверхность натяжения радиуса 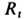 по Гиббсу), то ур-ние (15) обращается в обычное ур-ние Лапласа:
по Гиббсу), то ур-ние (15) обращается в обычное ур-ние Лапласа: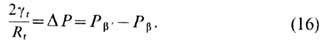
М е т о д с л о я к о н е ч н о й т о л щ и н ы используется при термодинамич. описании ТЖП в том случае, когда толщина плёнки H- измеряемый параметр. Условно полагают, что объём ТЖП Vf = AH заполнен жидкой фазой a, а объём Vb=V-Vf -текучей фазой b. Давление в референтной жидкой фазе a внутри плёнки полагают равным давлению Pa в объёмной фазе a, а все экстенсивные параметры представляют в виде суммы соответствующих параметров, отнесённых к объёмным фазам a и b,и поверхностных избытков, отнесённых к двум разделяющим поверхностям площади А:
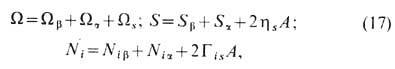
где Г is -величина адсорбции i -го компонента (удельного избытка числа молей i -го компонента, отнесённого к одной из разделяющих поверхностей), hs -межфазная энтропия при толщине плёнки H. Фундам. термодинамич. ур-ние для двух разделяющих поверхностей плоскопараллельной плёнки толщиной H
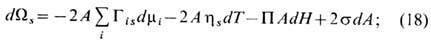


где s-межфазное натяжение, П - расклинивающее давление. T. о., в рамках метода слоя конечной толщины допустима механич. интерпретация s (как отнесённой к единице длины избыточной поверхностной силы, действующей параллельно поверхности плёнки) и П (как отнесённой к единице площади и направленной перпендикулярно к ТЖП силы взаимодействия между разделяющими поверхностями в плёнке).
Для симметричной плоской ТЖП межфазное натяжение s, вычисляемое как поверхностный избыток объёмного тензора напряжений со стороны объёмных фаз a и b , отнесённый к одной из разделяющих поверхностей в ТЖП (рис. 3, г):
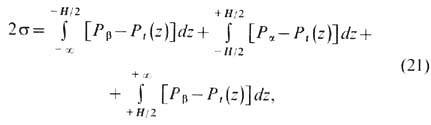
зависит от субъективного выбора толщины плёнки H. В отличие от s, расклинивающее давление П, к-рое при данном физ. состоянии ТЖП однозначно определяется давлениями Pa. и Pb является инвариантом, не зависящим от способа определения H. Из ур-ния (18)
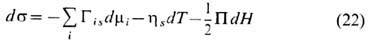
и можно получить ур-ние, связывающее s и П:
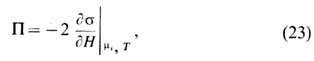
к-рое в термодинамике ТЖП наз. ур-нием Гиббса - Дюгема.
При разведении межфазных поверхностей плёнки на бесконечно большое расстояние, отвечающее условию П = 0, ур-ние (22) обращается в известное ур-ние Гиббса - Дюге-ма для плоских (невзаимодействующих) межфазных поверхностей:
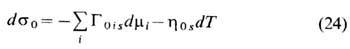
(индекс "0" означает отсутствие взаимодействия между поверхностями). Работа силы расклинивающего давления П при разведении разделяющих поверхностей единичной площади от H до бесконечности (при постоянных mi и T )наз. удельной свободной энергией взаимодействия в ТЖП толщины H. Она равна
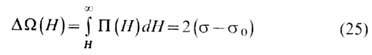
и инвариантна относительно локализации разделяющих поверхностей в ТЖП, т. е. не зависит от выбора способа определения толщины плёнки в методе слоя конечной толщины.
Линейное натяжение в ТЖП. Термодинамич. описание микроскопически малых ТЖП [напр., круглых ТЖП, возникающих между двумя капельками эмульсии (рис. 4, а)]требует учёта неоднородности поверхностных сил, действующих в т. н. переходной области плёнки, т. е. в той области, где плёнку уже нельзя назвать тонкой. Если в плоскопараллельной области расклинивающее давление П положительно и постоянно по величине, то в переходной области, где разделяющие фазы поверхности начинают искривляться, расклинивающее давление испытывает резкое изменение как по величине, так и по знаку, обращаясь в нуль в области объёмной фазы a. Профиль Н(r )плёнки в этой области становится сложной ф-цией переменного расклинивающего давления, так же, как и межфазное натяжение s, определяемое из ур-ния (25).
Вследствие невозможности в большинстве случаев точного измерения действит. профиля плёнки Н(r )принято использовать разл. референтные модели ТЖП в этой области, к-рые основаны на использовании т. н. идеализированного профиля плёнки Н и(r), совпадающего, по определению, с профилем поверхности, имеющей постоянные ср. кривизну и межфазное натяжение s0 в области объёмной фазы a, и экстраполируемого на переходную область при условии равенства нулю П.
При отрицат. уд. свободной энергии взаимодействия DW(Hf) где Hf -толщина плоскопараллельной области круглой симметричной плёнки, идеализированный профиль Н и(r )образует с плоскостью плёнки контактный угол qf, при этом rf принято считать радиусом круглой плёнки. В этом случае используют референтную модель, основанную на представлении о плёнке как о слое жидкой фазы a конечной толщиной Hf (рис. 4), ограниченном двумя круглыми разделяющими поверхностями радиусом rf каждая, характеризующимися межфазным натяжением sf=s(Hf) определяемым ур-нием (25), и двумя боковыми поверхностями с постоянной средней кривизной и межфазным натяжением s0, ограничивающими переходную область.
Представляя свободную энергию (большой термодинамич. потенциал W и при постоянных mi и T) референтной модели ТЖП в виде суммы объёмной (WV), поверхностной (WA) и линейной (WL) частей
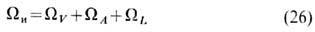
и используя условие энергетич. эквивалентности реальной ТЖП и её референтной модели W=W и , получаем
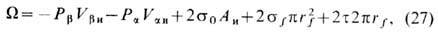
где
 и
и 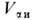 -объёмы фаз, А и - площадь боковой поверхности референтной модели, t-линейное натяжение (является по смыслу линейным избытком WL свободной энергии системы, отнесённым к длине окружности плёнки радиусом rf и имеющим размерность [Дж/м]).
-объёмы фаз, А и - площадь боковой поверхности референтной модели, t-линейное натяжение (является по смыслу линейным избытком WL свободной энергии системы, отнесённым к длине окружности плёнки радиусом rf и имеющим размерность [Дж/м]).
Из ур-ния (27) вытекает условие механич. равновесия контактной (разделяющей по Гиббсу) линии радиусом rf под действием поверхностных сил:
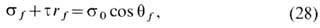
к-рое допускает механич. интерпретацию линейного натяжения как силы, действующей вдоль контактной линии, стремящейся её удлинить (при t>0 или сократить (при t>0).
Если идеализированный профиль H и(r) пересекает плоскость z = 0 в точке rf0. под контактным углом q0, то используют т. н. мембранную модель ТЖП (рис. 4, б); в этом случае выражение для свободной энергии примет вид
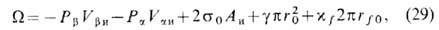
где
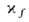 -линейное натяжение мембраны (по смыслу - линейный избыток WL свободной энергии системы, отнесённый к длине окружности мембраны радиусом rf0 и имеющий размерность [Дж/м]). Соответствующее уравнение механич. равновесия контактной линии примет вид
-линейное натяжение мембраны (по смыслу - линейный избыток WL свободной энергии системы, отнесённый к длине окружности мембраны радиусом rf0 и имеющий размерность [Дж/м]). Соответствующее уравнение механич. равновесия контактной линии примет вид
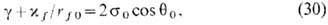
допускающий динамич. интерпретацию
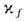 как силы, растягивающей (при
как силы, растягивающей (при 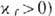 или сжимающей (при
или сжимающей (при 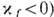 контактную линию, а
контактную линию, а 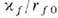 -как "двумерного капиллярного давления", действующего в плоскости мембраны. Ур-ния (28) и (30) обычно используются для эксперим. определения линейных натяжений
-как "двумерного капиллярного давления", действующего в плоскости мембраны. Ур-ния (28) и (30) обычно используются для эксперим. определения линейных натяжений 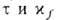 путём измерения зависимости контактных углов qf и q0 от радиусов rf и rf0 круглой плёнки.
путём измерения зависимости контактных углов qf и q0 от радиусов rf и rf0 круглой плёнки.
Несмотря на чрезвычайно низкие абс. значения линейного натяжения (согласно различным оценкам,
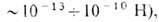 его вклад в энергетику процессов, происходящих в коллоидных системах, размеры частиц в к-рых менее 10-7 м (напр., при гетерогенном зародыше-образовании на твёрдых и жидких субстратах, нуклеаци-онном образовании дырок в мембранах, адгезии жидких и газообразных коллоидных частиц и др.), может оказаться существенным и требующим учёта.
его вклад в энергетику процессов, происходящих в коллоидных системах, размеры частиц в к-рых менее 10-7 м (напр., при гетерогенном зародыше-образовании на твёрдых и жидких субстратах, нуклеаци-онном образовании дырок в мембранах, адгезии жидких и газообразных коллоидных частиц и др.), может оказаться существенным и требующим учёта.
Лит.: Бабак В. Г., Термодинамика плоскопараллельных эмульсионных и пенных пленок, "Успехи химии", 1993, т. 62, № 1, с. 14; его же, Термодинамика свободных и взаимодействующих искривленных межфазных поверхностей в жидких пленках, там же, 1993, т. 62, № 8, с. 747; его же, Стерическая стабилизация микроскопических жидких пленок адсорбционными слоями полимеров, там же, 1994, т. 63, № 3, с. 228; его же, Линейное натяжение в термодинамике тонких жидких пленок, там же, 1992, т. 61, № 10, с. 1777; Rowlinson J. S., Widom В., Molecular theory of capillarity, Oxf., 1982; Thin liquid films. Fundamentals and Applications. Ed. I. B. Ivanov, N. Y.- Basel, 1988. В. Г. Бабак.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
