МАЛОУГЛОВОЕ РАССЕЯНИЕ

МАЛОУГЛОВОЕ РАССЕЯНИЕ

- упругое рассеяние эл.-магн. излучения или пучка частиц (электронов, нейтронов) на неоднородностях вещества, размеры к-рых существенно превышают длину волны излучения (или дебройлевскую длину волны частиц); направления рассеянных лучей при этом лишь незначительно (на малые углы) отклоняются от направления падающего луча. В зависимости от параметров излучения M. р. может быть обнаружено при рассеянии на неоднородностях разл. масштабов: от 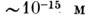и менее (рассеяние электронов на ядрах) до метров и километров (рассеяние радиоволн на неоднородностях земной поверхности). Распределение интенсивности рассеянного излучения зависит от строения рассеивателя, что используется для изучения структуры вещества.

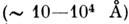В структурных исследованиях вещества используют, как правило, рентг. излучение или тепловые нейтроны с длиной волны (10 ^-1 - 1 HM). С их по-мошью изучают неоднородности коллоидных размеров . В отличие от др. дифракц. методов ( рентгеновского структурного анализа, нейтронографии, электронографии), с помощью M. р. исследуют структуру разупорядоченных объектов. Иногда M. р.- единств, метод получения прямой структурной информации о системах с хаотическим расположением неод-нородностей коллоидных размеров; наличие M. р. уже является доказательством присутствия в среде таких неоднородностей. Неоднородности же, имеющие размеры порядка межатомных расстояний, на малоугловой части дифракц. картины не сказываются.

С помощью M. р. изучают строение биол. молекул в растворе, объёмные дефекты в кристаллич. веществах, кластерную структуру жидкостей и аморфных тел, поры в разл. пористых материалах и т. д.

Возникновение метода M. р. связано с работами А. Гинье (A. Guinier) по изучению надмолекулярного строения сплавов (1938). В 1950-х гг. Г. Пород (G. Po-rod), O. Кратки (О. Kratky) и В. Луззати (V. Luzzati) развили теоретич. основы метода и разработали принципы конструирования установок для M. р. С кон. 1960-х гг. начался новый этап развития M. р., к-рый характеризуется широким применением нейтронного и синхротронного излучений и позиционно-чувствит. детекторов, а также новых методов анализа данных (вариация контраста, аномальное рассеяние, прямые методы).

Основы теории малоуглового рассеяния. При рассеянии излучения на неоднородностях с линейным размером D осн. доля рассеянного излучения сосредоточена в области векторов рассеяния:

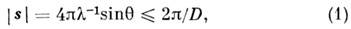
где 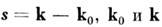- соответственно волновые векторы падающей и рассеянной волн,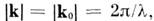

2Q - угол рассеяния, l - длина волны падающего излучения. Если 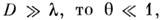т. е. рассеянное излучение сосредоточено вблизи первичного пучка. Интенсивность /(s) излучения, рассеянного разупоря-доченным ансамблем N идентичных атомов (мотивов атомов) с рассеивающей способностью (формфактором, см. А томный фактор)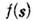, равна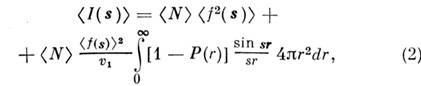

где знак (...) означает усреднение по ансамблю .N частиц, 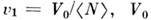- облучаемый объём образца, Р(r)- т. н. парная корреляц. ф-ция, r- расстояние между частицами. Первый член в (2) отвечает независимому рассеянию на мотивах атомов, второй - интерференции при рассеянии на этих мотивах.

Рассеивающие мотивы атомов иногда можно рассматривать как нек-рые частицы, включённые в однородную матрицу осн. вещества. Тогда ур-ние (2) соответствует т. н. разностной кривой рассеяния (разности ин-тенсивностей излучений рассеянного всей системой и рассеянного матрицей осн. вещества). Если описывать рассеивающие мотивы атомов ф-цией распределения рассеивающей плотности 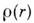, а плотность частиц матрицы обозначить 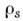, то разность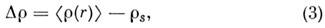

являющаяся интегральной характеристикой объекта, показывает, насколько эти частицы "выделяются" на фоне окружающей среды; эта разность наз. контрастом частицы относительно матрицы.

Бели p_s мало, то 2-м членом в (2) можно пренебречь (или исключить его с помощью последоват. экспериментов с веществами, характеризующимися различными 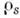). В этом случае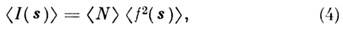

т. н. интенсивность M. р. пропорциональна усреднённой по всем направлениям интенсивности рассеяния одной частицей. Если частицы неидентичны, то

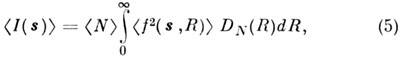
где R - нек-рый характерный размер частицы, 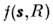- формфактор частицы с этим размером, 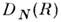- распределение частиц по R.

В тех случаях, когда систему нельзя представить в виде рассеивающих мотивов атомов, вкрапленных в матрицу осн. вещества, M. р. может быть вызвано разл. причинами. Так, в однофазных объектах (напр., в жидкости) M. р. может быть обусловлено статистич. флуктуациями плотности, причём

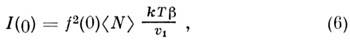
где 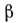- коэф. изотермич. сжимаемости жидкости. Если система многофазная, рассеяние возникает как за счёт флуктуации плотности, так и вследствие различия плотностей рассеивающих фаз. Для бинарных систем изотропное рассеяние на флуктуациях состоит из двух членов 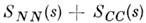, первый из к-рых обусловлен флуктуациями плотности, второй - флуктуациями концентраций. При резких границах фаз в качестве контраста будет выступать среднеквадратичная флуктуация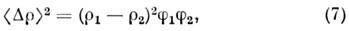

где 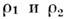- плотности рассеивающих фаз, 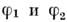- их объёмные доли, 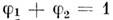. В этом случае M. р. даёт информацию об интегральных характеристиках объекта (объёмные доли фаз, поверхность раздела и др.).

Интерпретация данных малоуглового рассеяния. Для изотропных монодисперсных систем усреднённая по всем ориентациям интенсивность рассеянного частицей излучения запишется в виде

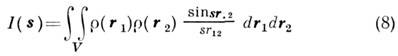
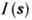(ф-ла Дебая). Здесь интегрирование ведётся в пределах объёма частицы . Интенсивность связана с усреднённой самосвёрткой плотности (корреляц. ф-цией) частиц соотношением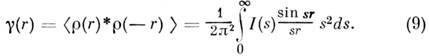

Ф-ции 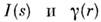для простейшего случая однородного шара приведены на рис. 1, 2. Из кривой рассеяния можно определить ряд интегральных параметров частицы (т. e. инвариантов).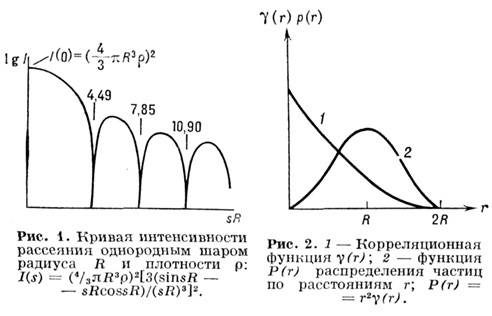

При 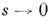имеем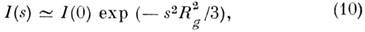

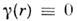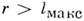R_g- радиус инерции частицы (ф-ла Гинье); из условия при определяется её макс, размер l _макс. T. н. инвариант Порода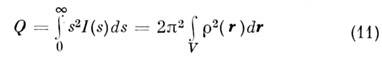

пропорционален квадрату контраста частицы относительно матрицы. При условии однородности частиц можно, кроме этого, определить её объём:

а также асимптотич. убывание I(s) при

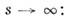
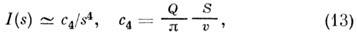
где S- площадь поверхности частицы. Для сильно вытянутых и сильно сплющенных частиц можно определять соответственно параметры поперечного сечения и толщины.

При заданных инвариантах кривая рассеяния существенно зависит от формы частицы (рис. 3). Это служит основой для метода моделей, где с учётом вычисленных инвариантов и информации, полученной др. методами, рассчитываются интенсивности рассеяния неск. (как правило, однородными) моделями и сравниваются с экспериментом.

Дополнит, информацию о внутр. структуре частицы можно получить с помощью т. н. метода вариации контраста. При изменении рассеивающей плотности матрицы справедлива ф-ла

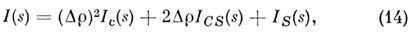
где 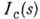- рассеяние "формой" частицы,- 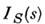рассеяние на её неоднородностях (т. е. при 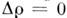), 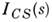- перекрёстный член. Аналогичные зависимости можно записать и для инвариантов. Для многокомпонентных частиц можно также "заменить" одну, из компонент (поместив рассеивающие частицы в среду с плотностью, равной плотности этой компоненты) аналогично тому, как это делается в оптике (см. Иммерсионный метод), и наблюдать рассеяние на остальных компонентах.

Вариация контраста может быть применена и в несколько другом виде, когда изменяют не плотность матрицы, а плотность отд. участков частицы и, анализируя изменения в кривой рассеяния, находят расстояние между этими участками. В M. р. рентг. излучения для этого присоединяют к частице тяжелоатомные метки (вводят в молекулы тяжёлые атомы), в M. р. нейтронов применяют изотопное замещение.

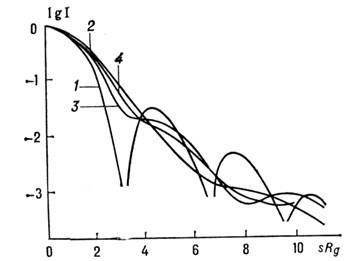
Рис. 3. Нормированные интенсивности малоуглового рассеяния частицами различной формы с одинаковыми R₃ и v:.1- шаровой слой; 2- трёхосный эллипсоид с отношением осей 0,5 : 1 : 1,5 ; 3- четыре соприкасающихся эллипсоида вращения; 4 - литая модель по мотивам модели 3.

Вариаций контраста удаётся добиться в рентгеновских экспериментах также с использованием аномального пропускания эффекта.

Существуют также прямые методы интерпретации интенсивности M. р., где при определ. ограничениях удаётся восстанавливать структуру частиц - ф-цию р(г). Простейший случай - сферически-симметричная частица. В этом случае

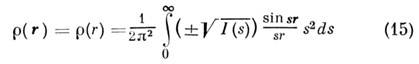
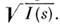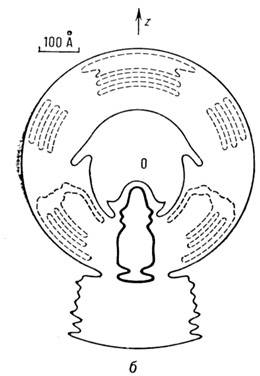
и для восстановления структуры требуется установить знак для амплитуд рассеяния Для аксиально-симметричных частиц удаётся с помощью разложения по сферическим гармоникам синтезировать ограниченное число возможных решений, выбор между которыми ведётся с помощью дополнит, информации.

Осн. класс монодисперсных объектов, изучаемых методом M. р.,- растворы биополимеров и их комплексов. Метод позволяет определять общие геометрические и весовые характеристики биол. частиц, их форму, а иногда и детали внутр. структуры. На рис. 4 приведён пример восстановления структуры бактериального вируса в растворе с помощью прямого метода.

Для полидисперсных систем частиц наиб, актуальна задача восстановления ф-ции распределения по размерам 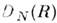из ур-ния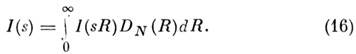

Функцию 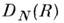определяют методом M. р. для раствора полимеров, пористых материалов, металлов и сплавов и т. д.

Помимо этого, возможно определение усреднённых по ансамблю значений инвариантов, с помощью к-рых рассчитываются общие характеристики дисперсной фазы.

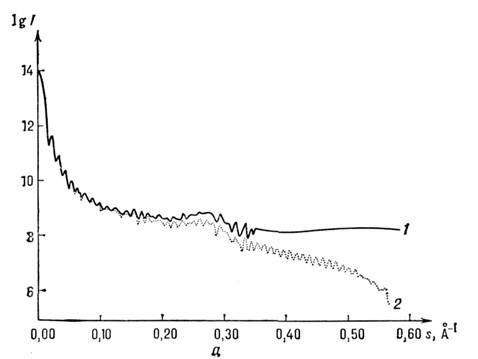
Рис. 4. a - Кривые рентгеновского малоуглового рассеяния бактериофагом Т7 в растворе (1- экспериментальная кривая; 2- рассеяние восстановленной структурой) ; б- восстановленная по данным малоуглового рассеяния структура Т7; рассчитанная в аксиально-симметричном приближении карта плек-тронной плотности (сечение, содержащее ось вращения г). Сплошные изолинии соответствуют электронной плотности 0,38е·А ^-3 (гидратированный белок), штриховые -0,42е·А ^-3 (сильногндратированная ДНК), жирная линия - 0,52е·А ^-3 (слабогидрати рованная ДНК).

В частности, для двухфазных систем

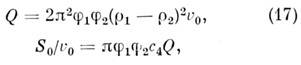
где S₀- площадь поверхности раздела фаз. Для получения дополнит, информации о системе используют разл. модификации методов вариации контраста.

M. р. используется также для определения строения частично упорядоченных объектов - т. н. ориентированных систем. В частности, при изучении слоевых структур (кристаллпч. полимеры, жидкие кристаллы, тонкие плёнки) по меридиональным рефлексам определяются толщина слоев D и профиль рассеивающей плотности по нормали к плоскости слоя р(х).

Для центросимметричного случая

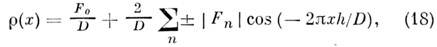
где F_n- амплитуда n-го рефлекса.

Знание профиля электронной плотности позволяет исследовать детали упаковки молекул разного сорта, в частности мультислоевьши структурами. На рис. 5 и 6 приведены рентгенограммы M. р. и распределение р(х )для сверхрешётки из двух видов молекул бсгена-га бария и октадецилфенола.

Техника эксперимента. T. к. распределение интенсивности M. р. рентг. лучей и тепловых нейтронов измеряется под малыми углами, осн. требование к экс-перим. технике заключается в создании достаточно узкого нерасходящегося пучка первичного излучения.

Рис. 5. Малоугловые рентгенограммы ленгмюровских плёнок бегената бария (Бег. Ba) и октадецилфенола (ОДФ): 1- сверхрешётка с чередованием бислрёв Бег. Ba и ОДФ (10 слоев) ;2 - плёнка из бислоёв Бег. Ba; 3- плёнка из бислоёв ОДФ.

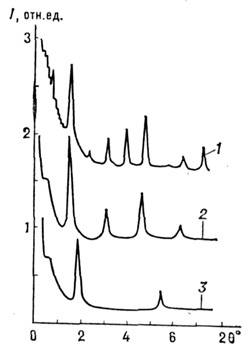
Рис. 6. Профиль электронной свсрхре-шетки (кривая J) и схема расположения молекул Бег. Ba и ОДФ в бислоях.

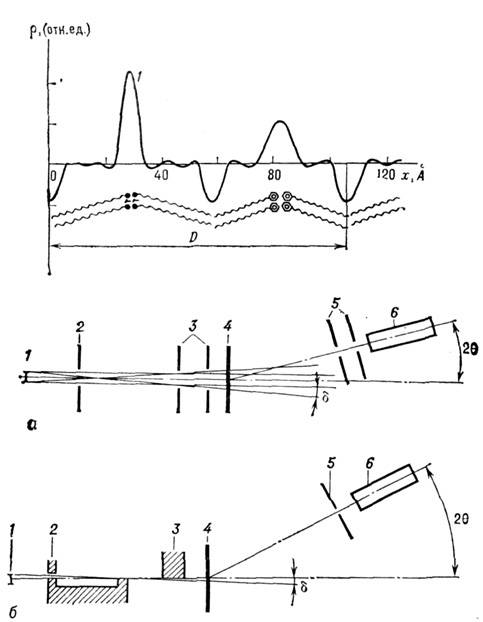
Период сверхрешётки

Рис. 7. Схемы малоугловых гониометров: о - трёхщелевая; б- по Кратки; 1- фокус источника; 2- формирующие щели; 3- щели образца; 4- образец; 5- приёмные щели; 6 - детектор (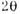- угол рассеяния; 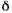- угловая расходимость падающего пучка).

Этого достигают с помощью спец. коллимац. систем и экранирования его паразитного рассеяния на краях щелей, окнами кювет с образцами, держателями, частицами воздуха на пути распространения луча и т. д. На рис. 7 a, б приведены наиболее распространённые схемы коллимации первичного пучка - трёхщелевая и схема блок-коллиматора по Кратки.

Источниками рентг. излучения в экспериментах M. р. служат как обычные рентг. трубки, так и трубки с вращающимся анодом, а также синхротронное излучение. Для регистрации рассеянного излучения используют одноканальные ионизац. счётчики; широкое распространение получают нозиционно-чувствительные детекторы, позволяющие регистрировать одновременно всю картину M. р. Источниками тепловых нейтронов служат спец. нейтронные реакторы.

Обработка экспериментальных данных. В приведённые выше соотношения между структурными характеристиками вещества и интенсивностью M. р. входит ф-ция 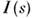- точная кривая рассеяния объектом. На практике всегда измеряется нек-рый дискретный набор данных 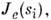содержащий разл. приборные искажения, фоновое рассеяние и статистич. шум. В общем виде для регистрируемой интенсивности рассеяния можно записать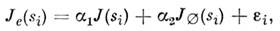

где 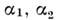- нормировочные константы,- 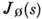рассеяние матрицей, деталями установки и пр.,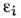- погрешности измерений. Кривая 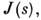несущая структурную информацию, отвечает "идеальной" кривой 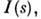"размытой" эффектами расходимости пучка и немонохроматичности излучения. Для изотропного рассеяния связь между 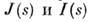записывается в виде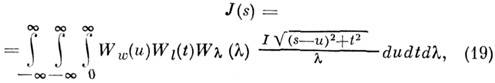

где 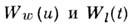- т. н. весовые ф-ции ширины и высоты коллимирующих щелей (приборные ф-ции прохождения вдоль и поперёк направления регистрации в плоскости приёмника), 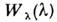- спектральная ф-ция (распределение по длинам волн излучения в падающем пучке). В реальных экспериментах искажения ф-ции 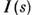могут быть весьма значительны (особенно из-за эффектов размытия на высоту щелей, в нейтронном рассеянии - из-за немонохроматичности излучения). Поэтому обработка данных, связанная с решением интегрального ур-ния (19), представляет собой, как правило, необходимый предварит, этап при извлечении структурной информации из данных M. р.

Лит.:Guinier A., Fournet G., Small-angle scattering of X-ray, N. Y.- L., 1955; Small-angle X-ray scattering, ed. by O. Glatter, O. Kratky, L., 1982; Останевич Ю. M., Сердюк И. Н., Нейтронографические исследования структуры биологических макромолекул, "УФН", 1982, т. 137, с. 85; Черемской П. Г., Методы исследования пористости твердых тел, M., 1985; Свергун Д. И., Fейгин Л. А., Рентгеновское и нейтронное малоугловое рассеяние, M., 1986; Фи-зико-химия многокомпонентных полимерных систем, под ред. Ю. С. Липатова, т. 1-2, К., 1986.

Д. И. Свергун, Л. А, Фейгин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.