СПИНОВОЕ СТЕКЛО

СПИНОВОЕ СТЕКЛО

- магнетик, в к-ром ниже определённой темп-ры(темн-ра замерзания T_f )возникает термодинамич. неравновесноеметастабильное магн. состояние (также наз. С. с.), к-рое характеризуется«замороженным» (отсутствуют термодинамич. флуктуации) пространств. распределениемориентации спиновых магн. моментов. Состояние С. с. вызывается, как правило, <наличием в системе хаотически расположенных магн. моментов, конкурирующих(т. е. имеющих разл. знаки, величину и пространственную зависимость) взаимодействийи обусловленной ими фрустрации магн. моментов (см. ниже), поэтомусостояние С. с. обычно возникает в неупорядоченных или аморфных магнетиках. Выше T_f С. с. переходит в равновесную магн. фазу (напр., парамагнитную).У любых веществ в состоянии С. с. существует ближний магн. порядок; дальниймагн. порядок может реализовываться (см. Асперомагнетизм, Сперимагнетизм )или отсутствовать (см. Сперомагнетизм). Неравновесность состоянияС. с. определяет зависимость его физ. параметров от времени, магн. и термич. <предыстории (как физ., так и технол.) данного образца, а также от степениоднородности, хим. чистоты и др. Всё это резко осложняет получение воспроизводимыхэксперим. результатов. Для С. с. характерны макроскопич. необратимые эффекты, <в т. ч. магнитная вязкость, магнитное старение, гистерезис магнитный и обусловленные ими явления магн. последействия и памяти.

Температурные зависимости статической магнитной восприимчивости сплава Си - Мп для 1,08 и 2,02 атомных% Мn. Участки а и с получены в поле 5,9 * 10^-4 Тл, которое былоприложено к образцам выше T_f ещё до их охлаждения. Участки bи d были получены после охлаждения образцов ниже T_f без магнитногополя и последующим повышением температуры в поле 5,9*10^-4 Тл.

Характерными признаками магнитного фазового перехода в состояние С. <с. в пост. внеш. магн. поле Н являются: возникновение при <T_f ималых H намагниченности т и её рост при понижениитемп-ры вплоть до Т _f, наличие при T = T_f резкогоизлома (быстро сглаживающегося с ростом Н )статич. магн. восприимчивости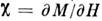 (рис.), линейный ход магн. составляющей теплоёмкости С при низких . и отсутствие особенности С при Т = T_f, отсутствиебрэгговских пиков в магнитном рассеянии нейтронов, критич. замедление спиновойдиффузии и др. При наблюдении перехода в фазу С. с. в переменном внеш. <магн. поле с частотой w обнаруживается ряд необычных для др. магн. фазявлений: частотная зависимость (дисперсия) темп-ры замерзания T_f, появлениемнимой части динамич. восприимчивости 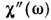, наличие долговременной (логарифмич.) релаксации магнитной и НЧ-шумов.

Состояние С. с. наблюдалось ещё с нач. 60-х гг. в разбавленных бинарныхметаллич. сплавах и твёрдых растворах , содержащих магн. ионы в немагн. матрице (А - магн. ион переходного металлаМп, Fе; В - немагн. ион благородного металла Ag, Au или меди) в определённоминтервале концентраций х; однако термин «С. с.» возник лишь последетальных работ В. Каннеллы и Дж. Мидоша (V. Carmella, J. Mydosh, 1972).Характерные для С. с. эксперим. результаты были получены на магн. диэлектрике 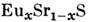при 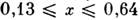(при х< 0,13 в образце возникает суперпарамагнетизм, апри х ферромагнетизм), на ряде бинарных и тройныхсистем, напр. на интерметаллич. сплавах переходных металлов друг с другом(Fe - Ni) и с редкоземельными металлами (Fе - ТЬ), редкоземельных сплавахтипа Y - Тb, La - Cd, метглассах, полупроводниках HgTe или CdTe, легированныхМп и др. Типичные магн. фазовые диаграммы с состоянием С. с. см. на рис.5-8 в ст. Магнитный фазовый переход.

К проявляющимся в этих веществах конкурирующим взаимодействиям, влияющимна установление разл. видов магн. упорядочения, относятся: обменноевзаимодействие и косвенное обменное взаимодействие ферро-и антиферромагн. <характера; зависящее от взаимной ориентации магн. моментов диполь-дипольноевзаимодействие; осциллирующее РККИ-обменное взаимодействие. Врегулярных кристаллич. структурах такие взаимодействия могут приводитьк появлению сложной неколлинеарной магнитной атомной структуры (вт. ч. несоизмеримой). В нерегулярных твердотельных системах (аморфных веществах, <неупорядоченных двух-или многокомпонентных сплавах и твёрдых растворах)благодаря конкуренции и хаотич. взаимному расположению магн. и примесныхионов (вызывающих иногда случайное изменение локальной оси магн. анизотропии)возникает фрустрация магн. моментов, приводящая к образованию состоянияС. с. В этом случае для расчёта наблюдаемых физ. величин кроме обычноготермодинамич. усреднения по ансамблю систем с Гиббса распределением вероятности(обозначаемого ) необходимо дополнит. усреднение (обозначаемое чертой сверху) по всемвозможным реализациям хаотич. расположения магн. моментов или набора взаимодействиймежду ними; при этом в качестве ф-ции распределения обычно выбирается комбинациядельта-функций или Гаусса распределение. Полное (но математическисложное) решение задачи усреднения по случайным конфигурациям для свободнойэнергии С. с. даёт т. н. метод реплик (от франц. replique - копия, образ).

В отличие от обычных магнитоупорядоченных фаз, в С. с. фрустрированноеосн. состояние имеет в пространстве конфигураций магн. моментов не одинглобальный минимум энергии (или при наличии вырождения небольшое их число, <ведущее к появлению магнитной доменной структуры), а макроскопич. <большое (растущее экспоненциально с ростом числа магн. моментов N) числолокальных минимумов (долин), обладающих иерархической (ультраметрической)структурой. Система магн. моментов С. с. испытывает случайную диффузиюв пространстве долин, преодолевая потенциальные барьеры разл. высоты (впределе больших N сколь угодно высокие). Этим объясняется практическинепрерывный широкий диапазон времён магн. релаксации (по теоретич. оценкам, <от 10^-12 до 10⁴⁰ с). В С. с. при Т = T_f благодаряфрустрации происходит переход системы магн. моментов в специфическое («замороженное»)состояние, характеризующееся спонтанным нарушением эргодичности,- подобнотому, как обычный фазовый переход связан со спонтанным нарушением соотв. <симметрии (см. Параметр порядка]. Практически неэргодичность означает, <что любое измерение магн. характеристики С. с. при конечных временах наблюденияописывает физ. свойства С. с. лишь в квазиравновесном состоянии, соотв. <пребыванию системы магн. моментов в одной или нескольких (но заведомо нево всех) долинах с вероятностями

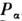
Обобщённым параметром порядка для С. с. может служить случайная ф-цияраспределения локальной намагниченности в узле i (в случае многих долин - ф-ция ).Обычно ограничиваются двумя её низшими моментами: ср. значением и дисперсией

Термодинамически сопряжённым параметром для q является дисперсия локального внеш. магн. поля h, причём статич. реакции функция , выражающаяся через нелинейную восприимчивость , имеет расходимость при Т = T_f. В случае, когда m =0 (идеальное С. с.), вместо q вводятся два параметра порядка и 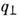, описывающиеанизотропию С. с., в случае кластерного или миктомагнитного (см. Миктомагнетизм )С. <с. в качестве параметров порядка используется набор корреляц. ф-ций , характеризующихближний магн. порядок.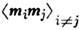Применяются и др. определения параметра порядка, существенно опирающиесяна неэргодичность С. с., напр. «однодолинного» типа [параметр Эдвардса - Андерсона (S. F. Edwards, P. W. Anderson), 1975],а также «двухдолинного» типа [параметр Паризи (G. Parisi), 1983], учитывающий перекрытие (корреляцию)двух долин и .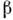

Теоретич. описание свойств С. с. весьма далеко от завершения, несмотряна значит. число аналитич. и компьютерных расчётов. Термодинамич. свойстваС. с. изучены достаточно хорошо в рамках модели Шеррингтона - Киркпатрика[ШК-модель (D. Sherrington, S. Kirkpatrick), 1975], представляющей собой среднегополя приближение для Изинга модели с дальнодействием. Обменныйинтеграл в этой модели не зависит от расстояния и является гауссовой случайнойвеличиной с ненулевым ср. значением. В рамках ШК-модели даётся качественноправильное при малых Н описание поведения 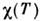, т(Т )и q(Т). Де Альмейда и Д. Таулес (De Almeida, D. Thouless,1978) установили границу устойчивости решения ШК-модели [линия Т(Н)~H^3/2 в фазовой плоскости ( Н, <Т)]; Паризи (G. Parisi,1980) усовершенствовал метод реплик, учтя переходы между долинами, и получилрешение, пригодное во всей плоскости ( Т, <Н). Существует много обобщенийШК-мрдели на случай учёта разл. типов анизотропии, размерности решёткиили параметра порядка, а также радиуса взаимодействия; при этом широкоиспользуются Ландау теория и метод ренормализационной группы. Динамич. <свойства С. с. получили теоретич. описание как в рамках традиц. подходовстохастич. динамики для индивидуальных спинов, так и с помощью зависящегоот времени континуального интеграла, позволяющего избежать введения методареплик.

Состояние С. с. не только проявляет необычные магн. свойства, но и служитхорошей моделью для ряда интересных задач в смежных областях науки, напр. <для локальных калибровочных полей Янга - Миллса в теории элементарныхчастиц, для нек-рых комбинаторных задач теории графов, теории оптимизациии организации параллельных вычислений в компьютерных сетях. Большой интересС. с. представляет в связи с введённой на его основе моделью действия нейронныхсетей при организации нелокальной памяти, устойчивой к дефектам структурыи обладающей точностью и быстротой обработки информации.

Лит.: Хёрд К. М., Многообразие видов магнитного упорядоченияв твердых телах, «УФН», 1984, т. 142, в. 2, с. 331; Коренблит И. Я., ШендерЕ. Ф., Спиновые отекла, М., 1984; Методы Монте-Карло в статистической физике, <пер. с англ., М., 1982; К и н ц е л ь В., Спиновые стекла как модельныесистемы для нейронных сетей, «УФН», 1987, т. 152, в. 1, с. 123; ГинзбургС. Л., Необратимые явления в спиновых стеклах, М., 1989; Р i s с h е rК. Н., Н е r t z I. A., Spin glasses, Cambr., 1991; Доценко В. С., «УФН»,1993, т. 163, с. 1. Ю. Г. Рудой.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.