СПЕКТР ОПЕРАТОРА

СПЕКТР ОПЕРАТОРА

- обобщение на бесконечномерный случай понятиямножества собственных значений матрицы линейного преобразованияв конечномерном векторном пространстве.

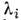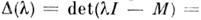Если М - такая n X n-матрица, то её собств. значения - это комплексные числа, для к-рых ур-пие имеет ненулевые решения ( собственные векторы матрицы М). Длясуществования таких решений необходимо и достаточно, чтобы 0, где I - единичная пX п -матрица. Множество собств. <значений (спектр М )содержит не более п точек, т. к.- полином степени и и имеет не более п различных корней .Сама матрица М удовлетворяет ур-нию Гамильтона - Кэли 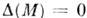,а по теореме Виета 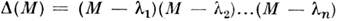(для простоты принято, что все 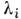различны). Если положить 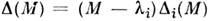, то оператор 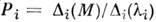является проектором на собств. подпространство, принадлежащее 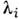:для любого вектора х вектор P_i(x)- собственныйи принадлежит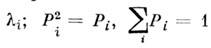

При этом матрица М имеет спектральное разложение [1]:

Для эрмитовых М проекторы также эрмитовы,вещественны, а собств. подпространства ортогональны друг другу. При 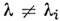матрица имеет обратную. Вообще, в конечномерном случае есть две возможности: либо(I)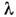 -регулярная точка и резольвента 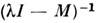существует как оператор на всём векторном пространстве, либо (II)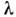- точка спектра и резольвента не существует.

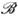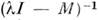В бесконечномерном случае речь идёт об операторах А, действующихв нормированном линейном пространстве (банаховом пространстве),и появляется третья возможность: (III) ур-ние имеет лишь нулевые решения в ,но резольвента не определена на всём .Объединяя вторую (т о ч е ч н ы й, или дискретный, спектр) и третью (непрерывныйи остаточный спектры) возможности, С. о. 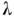называют множество таких ,для к-рых резольвента не является ограниченным оператором на всём .При этом принадлежит непрерывному спектру, если область значений оператора плотна в ,и остаточному - в противном случае. У ограниченных самосопряжённых операторовостаточный спектр отсутствует.

В квантовой механике наблюдаемым отвечают самосопряжённые операторы, <действующие в гильбертовом пространстве . Сведения об их спектре имеют непосредственный физ. смысл. Так, точечныйспектр оператора Гамильтона - это уровни энергии связанных состояний, анепрерывному спектру отвечают состояния, фигурирующие в теории рассеяния. <В соответствии с идеей П. Дирака [2] в квантовой механике оперируют с формальнымирешениями ур-ния , отвечающими непрерывному спектру; такие решения не принадлежат 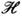.Напр., для системы с одной степенью свободы, координата к-рой может приниматьзначения на всей оси ,, в координатномпредставлении реализуется как пространство 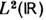квадратично интегрируемых ф-ций на 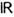. Операторимпульса 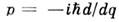имеетнепрерывный спектр, совпадающий с 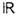.Решениями ур-ния являются плоские волны ;поскольку в пространстве их норма 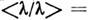расходится, они не принадлежат 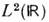и наз. обобщёнными собственными векторами. Комбинация является аналогом проектора на обобщённый собств. вектор 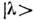, а спектральное разложение

аналогом разложения (*) для случая непрерывного спектра: для любоговектора из имеем: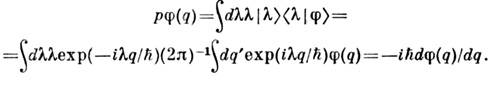

Эта конструкция служит только моделью математически строгого определенияспектрального разложения операторов с непрерывным спектром ([3], [4]).В большинстве квантовомеханич. задач дискретный и непрерывный участки спектране пересекаются, а случаи, когда точки дискретного спектра погружены внепрерывный, считаются экзотическими. Простейший пример такой ситуации- осциллирующий и медленно убывающий с расстоянием потенциал (т. н. потенциалВигнера - фон Неймана).

Лит.:1) X а л м о ш П., Конечномерные векторные пространства, <пер. с англ., М., 1963; 2) Д и р а к П. А. М., Принципы квантовой механики, <пер. с англ., 2 изд., М., 1979; 3) Р и д М., Саймон Б., Методы современнойматематической физики, т. 1, Функциональный анализ, пер. с англ., М., 1977;4) ф о н Нейман И., Математические основы квантовой механики, пер. с нем.,М., 1964. В. П. Павлов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.