РЕГРЕССИОННЫЙ АНАЛИЗ

РЕГРЕССИОННЫЙ АНАЛИЗ

- раздел матем. статистики, посвящённый методам анализа зависимости одной физ. величины Y от другой - х. Пусть в точках х _п независимой переменной x получены измерения Y_n. Нужно найти зависимость ср. значения величины 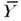от величины х, т. е. 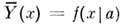, где a - вектор неизвестных параметров а _i (т. е. вектор, компонентами к-рого являются a_i). Ф-цию 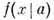наз. ф-цией регрессии. Обычно предполагают, что 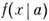является линейной ф-цией параметров а, т. е. имеет вид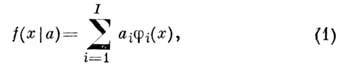

где f_i(x) - заданные ф-ции. В этом случае матрицу А _ni=f_i(x_n) наз. регрессионной матрицей. Для определения параметров a_i обычно используют наименьших квадратов метод, т. е. оценки a_i определяют из условия минимума функционала

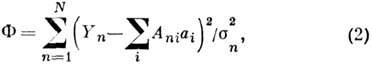
где - дисперсии ошибок измерений Y_n в предположении,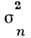что они не коррелированы, и из минимума функционала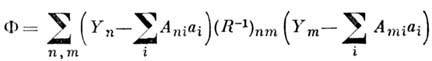

для коррелиров. измерений с корреляц. матрицей R. В качестве ф-ций f_i(x) при небольших I (I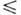5) обычно служат степенные ф-ции f_i(x)= xⁱ. Часто используют ортогональные и нормированные полиномы на множестве х _п: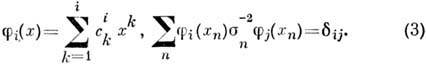

В этом случае легко найти оценку

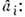
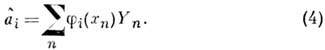
Отсюда следует, что вычисление 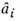не зависит от вычисления других .

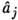Популярно использование в качестве f_i(x). сплайнов В _i(x), к-рые обладают двумя осн. свойствами: а) В _i(x)- полином заданной степени; б) В _i(x )отличен от нуля в огранич. окрестности точки х _i.

При поиске ф-ции регрессии в виде (1) естественно возникает вопрос о кол-ве членов I в сумме (1). При малом значении I нельзя достичь хорошего описания 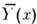, а при большом - велики статистич. ошибки ф-ции регрессии.

В предположении, что вектор ошибок измерений Y_n распределён нормально, можно использовать статистические критерии, ивыбрать то I, к-рое является оптимальным при данном множестве измерений Y_n. В случае, когда f_i(x) - ортогональные полиномы, это особенно просто. Как видно из (4), дисперсия 0_i равна 1 и по значению <Лит.: Клепиков Н. П., Соколов С. Н., Анализ и планирование экспериментов методом максимума правдоподобия, М., 1964; Кендалл М. Дж., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973; Се-бер Дж., Линейный регрессионный анализ, пер. с англ., М., 1980. В. П. Жигунов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.