ЭЛЕКТРОН-ФОНОННОЕ ВЗАИМОДЕЙСТВИЕ

ЭЛЕКТРОН-ФОНОННОЕ ВЗАИМОДЕЙСТВИЕ

- взаи-модействие между двумя подсистемами квазичастиц в твёрдых телах, а именно, носителями заряда ( блоховскими электронами в металлах, полупроводниках и диэлектриках или дырками в этих веществах) и тепловыми колебаниями кристаллич. решётки твёрдых тел - фоноиами. Конкретный вид гамильтониана Э.-ф. в. зависит от структуры кристалла, числа носителей заряда, характера зонного спектра и особенностей колебаний кристаллич. решётки.

Введение. В идеальной кристаллич. решётке все атомы или ионы узлов расположены строго периодически в пространстве и не двигаются (их можно считать "замороженными").

Однако даже при темп-ре абс. нуля ионы совершают нулевые колебания. При темп-pax, отличных от нуля, возникают хаотич. тепловые колебания ионов узлов решётки (см. Колебания кристаллической решётки). Рост темп-ры приводит в металлах к росту числа фононов и увеличению сопротивления току, что хорошо наблюдается в чистых металлах в нормальном состоянии. В полупроводниках рост темп-ры также приводит к росту числа носителей заряда. Э.-ф. в. оказывает существ. влияние на явления переноса в этих веществах, а также приводит к междолинным механизмам рассеяния электронов, ослаблению ультразвука, фононному увлечению и др. Кроме того, в кристаллич. решётках имеются отклонения от идеальности (см. Дефекты в к р и с т а л л а х), такие, как дислокации, межузельные атомы той же природы, что и осн. решётка, вакантные узлы, примесные атомы внедрения в междоузлиях и замещение атомов в узлах решётки посторонними атомами.

Квантовомеханич. теория Блоха движения электронов в идеальной замороженной кристаллич. решётке сводит сложную многоэлектронную проблему к задаче о движении отд. электрона под действием строго периодич. потенциала. Волновая ф-ция Блоха, определяющая это движение электрона, представляет собой модулированную с периодом идеальной решётки плоскую волну

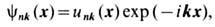
где n- дискретный номер энергетич. зоны, k - квазиволновой вектор, определённый с точностью до вектора обратной решётки К. Собственные значения энергии Е _n (k )также зависят от этих двух квантовых чисел n и k. Если кристалл имеет ограниченные размеры, то векторы k квазидискретные.

Поведение электронов или дырок в кристалле имеет особенно простой вид на краю изотропных зон, когда возможно использование т. н. приближения эфф. массы:

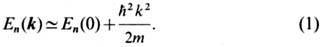
Существенно, что величина 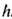k является не импульсом, а квазиимпульсом, и все законы сохранения квазиимпульса в процессах столкновения квазичастиц выполняются лишь с точностью до 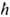К. Процессы, в к-рых векторы обратной решётки не участвуют, наз. н о р м а л ь н ы м и, а те, в к-рых 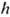К участвуют,- процессами п е р е б р о с а Пайерлса или u -процессами. Эти процессы имеют важное значение для установления термодинамич. равновесия в электрическом поле; в частности, электрон-электронные столкновения определяют электро- и теплопроводность кристаллов (см. Межэлектронное рассеяние).

T. о., в строго периодич. поле кристалла электроны и дырки на краю энергетич. зон ведут себя как свободные заряж. частицы с эфф. массой т. Под действием электрич. поля это привело бы к линейно возрастающей со временем скорости их трансляционного движения и к сколь угодно большим электрич. токам. Однако существуют тормозящие силы, действующие на носители тока в кристалле и ограничивающие их скорости. Причиной торможения являются процессы рассеяния электронов на всех отклонениях от идеальности кристаллич. решётки, так что протекание тока в кристалле сопровождается сопротивлением.

Особого рассмотрения требует явление сверхпроводимости, при к-ром наблюдается устойчивое к нарушениям решётки квантовое макроскопич. движение электронов. В нормальном, т. е. несверхпроводящем, состоянии вещества протекание электрич. тока всегда сопровождается сопротивлением, к-рое существенно зависит от темп-ры. Одной из причин такой зависимости является увеличение амплитуды тепловых колебаний ионов с ростом темп-ры T и усилением столкновений электронов с ними.

Колебания кристаллической решётки. Методы описания колебаний кристаллич. решётки вследствие тепловых движений ионов, находящихся в её узлах, основаны на разложении в ряд Тейлора потенц. энергии решётки U(... R_nj... )по степеням малых смещений u_nj ионов из их положения равновесия R_nj=R⁰_nj+u_nj; здесь п = п₁ а + п₂b + п₃ с - вектор, определяющий положение элементарной ячейки кристалла. Предполагается, что таких ячеек в кристалле N и в каждой ячейке имеется v ионов, положение к-рых в данной ячейке определяется векторами j. Векторы a, b, с определяют постоянные решётки по трём направлениям.

Разложение величины U по степеням смещений u_nj содержит гармонические, т. е. квадратичные, а также ангармонические- кубические и более высокие формы по этим векторам с соответствующими коэф. упругости. Простейшее приближение является квадратичным (см. Динамика кристаллической решётки). Оно диагонализуется в нормальных координатах, что приводит к определению 3v ветвей частот w_a(k) и ортов, определяющих направления нормальных колебаний системы. T. к. каждая величина k принимает N дискретных значений, то в гармонич. приближении имеем дело с 3vN независимыми гармонич. осцилляторами, описывающими в данном приближении колебания кристаллич. решётки. Энергия независимых осцилляторов имеет вид

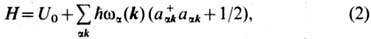
где a нумерует 3v ветвей спектра колебаний решётки, 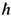w_a(k)- квант энергии колебаний кристаллич. решётки - фонон. Каждый фонон обладает квазиимпульсом 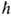k и энергией 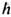w_a(k). Набор собств. частот колебаний решётки определяется только упругими свойствами решётки и массами атомных ядер.

Из 3v ветвей колебаний имеются З а к у с т и ч е с к и е, при к-рых смещения ионов элементарной ячейки происходят в фазе и элементарная ячейка смещается как единое целое. Эти колебания сопровождаются локальными сжатиями и разрежениями. При k = 0 частоты этих колебаний равны нулю. Если атомы элементарной ячейки смещаются в про-тивофазе, то они оставляют центр масс ячейки в покое, но вызывают смещение центров тяжести зарядов и сопровождаются появлением дипольного электрич. момента. Эти колебания оказываются оптически активными и наз. о пт и ч е с к и м и колебаниями. Соответствующие кванты наз. оптич. фононами: число их видов равно 3(v-1), причём при k = 0 энергии этих фононов не равны нулю.

T. о., в гармонич. приближении колеблющаяся кристаллич. решётка заменяется набором независимых фононов, свободно перемещающихся в кристалле. Энергия, переносимая фононами, перемещается с групповой скоростью фононов, и в этом приближении для потока тепла нет сопротивления.

В этом приближении нет также и теплового расширения кристалла, т. к. ср. смещение ионов равно нулю. Это хорошо видно, если учесть, что смещение ионов u_nj после разложения по плоским волнам оказывается линейной формой от безразмерных координат q_k или от импульсов p_k фононов:

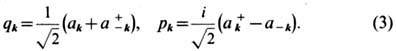
В континуальном пределе это разложение для смещения и( х )имеет вид

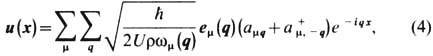
где e_m(q) - единичный вектор направления поляризации фонона, r - плотность вещества. Очевидно, что в гармонич. приближении ср. значение квантовых амплитуд рождения и уничтожения фононов а ⁺_q, а _q[и, следовательно, самого смещения u(x)] равно нулю. Благодаря ангармо-нич. слагаемым в разложении энергии решётки U, к-рые становятся весьма существенными при увеличении темп-ры, возникают процессы столкновения фононов с фононами, в к-рых участвуют три, четыре или большее число фононов. В результате этих процессов возникает теплосопротивление; кроме того, благодаря ангармониз-мам средние значения смещений ионов оказываются отличными от нуля, и это обусловливает тепловое расширение кристалла.

С помощью фононов рассеяние носителей заряда на тепловых колебаниях решётки можно описать на основе корпускулярных представлений. Обычно рассматривается подсистема, состоящая из свободных квазичастиц - носителей заряда, сталкивающаяся с подсистемой свободных фононов, что порождает квантовые переходы в системе. Строго говоря, следует учесть также кулоновское взаимодействие в подсистеме зарядов и ангармонич. взаимодействие в подсистеме фононов и др. факторы, влияющие на времена жизни квазичастиц и ограничивающие применимость простой концепции газов квазичастиц, сталкивающихся между собой.

Энергия Э.-ф. в. простейшего вида линейно зависит от деформации, возникающей при акустич. и оптич. колебаниях решётки. Ниже приводятся выражения для этой энергии, основанные на разл. физ. представлениях относительно характера взаимодействия электронов с решёткой.

Елоховское взаимодействие. Простейший вид Э.-ф. в. в металлах, согласно к-рому решётка металла рассматривается как статич. пространственно-периодич. поле V(x), а все электроны двигаются независимо, подчиняясь одноэлектронному ур-нию Шрёдингера,

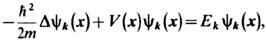
где y_k(x), E_k - собств. состояние и соответствующая собств. энергия электрона. Потенциал V(x), равный сумме потенциалов отд. ионов, обладает периодичностью решётки

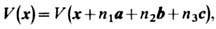
где a, b, с- базисные векторы решётки.

В отсутствие к.-л. нерегулярностей решётки электроны не испытывают никакого рассеяния. При тепловом движении ионов возникает поле смещений ионов и( х )от их положений равновесия. Согласно Блоху, при движении ионов происходит деформация плотности заряда электронов вокруг иона, причём действующий на электрон потенциал V_d (x' )в точке x'= x + и( х )деформированной решётки совпадает с потенциалом V_n ( х )в точке x недеформированной решётки, т. е. V_d ( х + и( х)) = V_n(x). Тогда действующий на электрон возмущающий потенциал в линейном по смещению ионов приближении равен

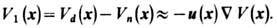
Наряду с концепцией Блоха существует концепция Нордгейма жёстких ионов, согласно к-рой окружение движущихся ионов почти не меняется, когда они совершают тепловые колебания, в этом случае вид действующего на электрон возмущающего потенциала будет иным. Гамильтониан Э.-ф. в. строится на основании полученного одно-электронного оператора возмущения с помощью правил для аддитивных квантовомеханич. величин (см. ниже), причём в блоховской модели существ. значение имеет поле продольных смещений решётки.

Метод потенциала деформации Бардина - Шокли. Э.-ф. в. в ковалентном полупроводнике можно найти, если считать концентрацию носителей заряда малой и пренебречь их взаимодействием между собой. Если в таком кристалле возникает небольшая статич. деформация, описываемая (в континуальном приближении) вектором смещения и( х), то соответствующий тензор деформаций имеет компоненты зависящие от координаты х элемента объёма. Обозначим через E₀(k )зонную энергию электрона до деформации среды. При малых концентрациях носителей представляет интерес область волновых векторов, близких к экстремумам энергетич. зон, где предполагается справедливым приближение эфф. массы (1). В присутствии пространственно-неоднородной деформации энергия электрона приобретает плавную зависимость от х вида

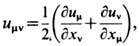
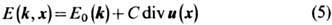
при условии, что E₀(k )имеет сферически-симметричный вид [в противном случае к правой части (5) следует добавить слагаемое, содержащее сдвиговые деформации]. Величина div u(x) описывает относит. изменение объёма системы, возникающее только при деформациях, обусловленных акустич. фононами, возникают дальнодействующие электростатич. потенциалы, не принимаемые здесь во внимание (см. ниже).

Гамильтониан Э.-ф. в. принимает вид

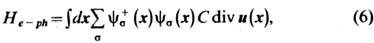
где s - спиновые индексы, y_s*, y_s - электронные операторы рождения и уничтожения соответственно. Разложим эти операторы по блоховским ф-циям и воспользуемся разложением (4) оператора смещений и( х). Поскольку divu(x) содержит скалярное произведение ke_m(k), равное нулю для поперечных нормальных колебаний, вклад в (6) даёт лишь продольная фононная мода. Окончательно для Э.-ф. в. получаем

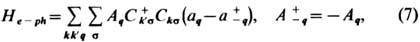
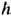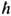где квазиволновые векторы электронов и фононов связаны между собой законом сохранения k' = k + q для нормальных процессов рассеяния и k' = k + q + K (где К- вектор обратной решётки) для процессов переброса Пайерлса. Гамильтониан Э.-ф. в. H_e-ph описывает процессы рассеяния, при к-рых уничтожаются электрон и фонов с квазиимпульсами k и q соответственно и рождается электрон с квазиимпульсом 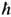k'. Второй член гамильтониана Э.-ф. в. описывает процесс уничтожения одного электрона с квазиимпульсом hk и рождения двух частиц - фонона и электрона с квазиимпульсам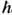и -q и 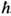k' соответственно. T. о., благодаря Э.-ф. в. электронные состояния всегда сопровождаются появлением фононов. Реальной частицей является не свободный блоховский электрон (или дырка), а электрон (дырка), окружённый облаком продольных акустич. фононов. Произошла вторичная перенормировка свойств электрона-на этот раз благодаря фононам. Эта новая квазичастица наз. поля-роном, хотя первоначально этот термин был введён для обозначения электрона, окружённого облаком продольных оптич. фононов в ионных кристаллах.

Процессы столкновения квазичастиц характеризуются также законом сохранения энергии к-рый выполняется для реальных частиц, существовавших в начале и в конце процесса взаимодействия (см. Рассеяние носителей заряда в кристаллических твёрдых телах).

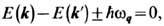
Взаимодействие с оптическими фононами. Оптич. колебания кристаллич. решётки сопровождаются возникновением дипольных моментов и поляризацией среды. В длинноволновом пределе кристаллич. решётку можно рассматривать как сплошную среду с непрерывным распределением поляризации р( х), к-рая совершает колебания с частотами оптич. фононов. Энергия взаимодействия заряда е, находящегося в точке x, с дипольным моментом р( х), находящимся в точке х', равна

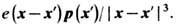
С учётом плотности пространств. распределения заряда

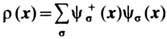
энергия Э.-ф. в. принимает вид

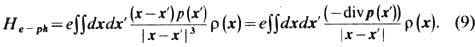
Повторяя применительно к div p( х )рассуждения, связанные с divu(x) в ф-ле (6), убеждаемся, что в Э.-ф. в. дают вклады только продольные волны. Следовательно, в длинноволновом пределе реализуется взаимодействие электронов только с продольными оптич. фононами.

Поляризация среды поддерживается электрич. полем [или, точнее, электрич. смещением D(x), создаваемым носителями заряда (см. Диэлектрики)]. Полная поляризация среды создаётся не только смещением ионов из положений равновесия (ионная поляризация), но и деформацией электронных оболочек ионов (электронная поляризация). Оба эти механизма поляризации возникают в присутствии ста-тич. электрич. поля и описываются статич. диэлектрической проницаемостьюe₀:

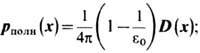
здесь p _полн - полный дипольный момент, создаваемый обоими факторами. Однако при исследовании электронно-колебат. взаимодействия, обусловленного оптич. фонона-ми, следует учесть только ионную поляризацию, так что из p _полн следует исключить электронную поляризацию р _эл(x), к-рая является безынерционной и удовлетворяет соотношению р _эл( х)=(4p)^-1.(1 - 1/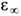)D(x), где 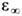является высокочастотной частью диэлектрич. проницаемости, равной квадрату показателя преломления света в среде.

Поэтому часть поляризации среды, обусловленная инерционным движением ионов, определяется разностью двух вышеприведённых величин:

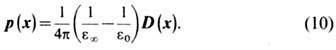
Далее, в (9) следует подставить разложение по плоским волнам продольной части вектора p(x):

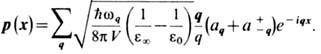
Гамильтониан Э.-ф. в. по-прежнему имеет вид (7), но коэффициенты A_q в данном случае имеют иной вид:

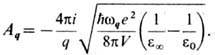
Модель Бардина - Пайнса. Простая модель Блоха для Э.-ф. в. в металле нуждается в уточнении ввиду значит. концентрации электронов проводимости и важности учёта межэлектронного взаимодействия, к-рое перенормирует осн. динамич. величины. Помимо экранировки кулонов-ского взаимодействия и замены закона 1/r на ехр (- k _эr)/r существенно меняется величина матричных элементов Э.-ф. в., а также характер закона дисперсии фононов.

Согласно более точной модели Бардина - Пайнса, электроны проводимости двигаются в непрерывной положительно заряженной среде и взаимодействуют как между собой по закону Кулона, так и с продольными колебаниями этой среды (фононами). Гамильтониан такой системы состоит из гамильтониана свободных блоховских электронов Н⁰_e, свободных фононов H⁰_ph, и двух слагаемых взаимодействия: H_e-ph является электрон-фононным, а Н _е-е- электрон-электронным кулоновским взаимодействием:

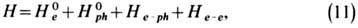
где

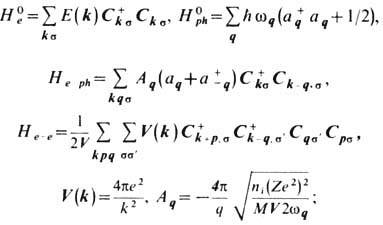
здесь M- масса иона, Ze- его заряд, V- объём системы, n_i = N_i/V- плотность ионов. Частота w_q продольных колебаний ионов обладает слабой дисперсией. При q = 0 эта частота равна плазменной ионной частоте

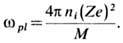
Отметим, что в рассматриваемой модели имеет место свойство

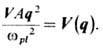
Модель Бардина - Пайнса учитывает наиб. существенные особенности металлов и приводит к качественно верному описанию Э.-ф. в. в них.

Лит.: Бете Г. А., Зоммерфельд А., Электронная теория металлов, пер. с нем., Л.- M., 1938; Зейтц Ф.. Современная теория твёрдого тела, пер. с англ., M.- Л., 1949; Пекар С. И., Исследования по электронной теории кристаллов, M.- Л., 1951; Пайерлс Р., Квантовая теория твердых тел, пер. с англ., M., 1956; Займан Дж., Электроны и фононы, пер. с англ., M., 1962; Пайнc Дж., Элементарные возбуждения в твёрдых телах, пер. с англ., M., 1965; Киттель Ч., Квантовая теория твёрдых тел, пер. с англ., M., 1967; Киреев П. С., Физика полупроводников, 2 изд., M., 1975; Ашкрофт H., Мермин H., Физика твёрдого тела, пер. с англ., т. 1-2, M.. 1979; Хакен X., Квантовая теория твёрдого тела, пер. с нем., M., 1980; Ридли Б., Квантовые процессы в полупроводниках, пер. с англ., M., 1986; Bardeen J., Pines D., Electron-phonon interaction in metals, "Phys. Rev.", 1955, v. 99, p. 1140; Bloch F., Quantum mechanics of electrone in crystal lattices, "Z. Phys.", 1928. Bd 52, S. 555.

В. А. Москаленко, Ю. Г. Рудой.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.