РАЗРЫВЫ МАГНИТОГИДРОДИНАМИЧЕСКИЕ

РАЗРЫВЫ МАГНИТОГИДРОДИНАМИЧЕСКИЕ

- тонкие переходные области, в к-рых происходит резкое изменение (скачок) магнитогидродинамич. (МГД-) параметров (давления, энтропии, плотности, скорости течения, магн. поля) или их производных. Р. м. возникают при столкновении двух потоков, обтекании тел (напр., обтекании планет солнечным ветром), взрывах (вспышках новых и сверхновых звёзд), при сжатии газа поршнем, внезапном включении эл.-магн. поля, изменении (исчезновении) начальных или граничных условий и т. д. Р. м. распространяются в идеальном газе (жидкости, плазме) с высокой (строго говоря, бесконечной) электрич. проводимостью в присутствии магн. поля. Если пренебречь эффектами неидеальности вещества (вязкостью, теплопроводностью, джоулевым нагревом), то толщина переходной области равна нулю, т. е. Р. ы. сосредоточены на поверхностях.

Различают слабые и сильные Р. м. Слабым наз. разрыв, на поверхности к-рого имеет место скачок к.-л. производных МГД-параметров как ф-ций координат при непрерывности самих параметров. Поверхности, на к-рых возможен слабый Р. м., являются харак-теристич. поверхностями ур-ний идеальной магнитной гидродинамики. Существует 7 типов слабых Р. м.: энтропийный, 2 альвеновских, 2 быстрых и 2 медленных магнитозвуковых. Слабые Р. м. движутся относительно среды со скоростью соответствующих линейных волн.

Р. м. наз. сильным, если на его поверхности имеет место скачок одного или неск. МГД-параметров. Сильный Р. м. может образоваться при пересечении слабых разрывов одного типа. Граничные условия на поверхности сильного Р. м., связывающие значения МГД-параметров по разные стороны разрыва, получаются из законов сохранения массы, импульса и энергии и ур-ний Максвелла в интегральной форме. В системе отсчёта, где сильный Р. м. покоится, они в изотропном случае имеют вид:

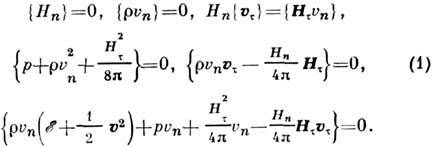
Здесь r, r и 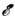- соответственно давление, плотность и уд. внутр. энергия вещества;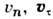и - нормальная и тангенциальная (относительно поверхности разрыва) компоненты соответственно скорости вещества и напряжённости магн. поля; скобки {f}обозначают скачок параметра f при переходе через поверхность разрыва, т. е. разность (f₂ - f₁) значений этого параметра за фронтом разрыва f₂ и перед ним f₁.

Различают 4 типа сильных Р. м.: тангенциальный, контактный, альвеновский и ударные волны. Для тангенциального разрыва поток вещества через поверхность разрыва отсутствует (u_h= 0), а магн. поле параллельно поверхности разрыва ( Н _п=0). На тангенциальном Р. м. плотность r и тангенциальная скорость u _т имеют скачки произвольной величины, а скачки давления p и магн. поля H _т связаны соотношением:

В анизотропном случае, когда скачок произвольной величины может иметь продольное давление Р _||, а скачки поперечного давления p_^ и магн. поля связаны соотношением (2).

Тангенциальным разрывом является поверхность раздела двух жидкостей с разл. термодинамич. параметрами, движущимися относительно друг друга с нек-рой скоростью, параллельной границе раздела. Примером тангенциального Р. м. служит магнитопау-за как граница раздела между магнитосферой и солнечным ветром. На тангенциальном разрыве обычно развивается неустойчивость Кельвина - Гельмгольца с инкрементом

Она может быть застабилизирована достаточно сильным магн. полем

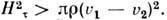
Контактный разрыв покоится относительно среды (u_n = 0), однако магн. поле имеет нормальную компоненту (0). На поверхности контактного Р. м. непрерывны давление р, магн. поле Н, скорость u _т, а плотность r и др. термодинамич. параметры могут испытывать произвольные скачки. В анизотропном случае,, давление и тангенциальная компонента магн. поля могут иметь на контактном разрыве скачки, удовлетворяющие соотношениям:

На альвеновском (вращательном) разрыве плотность среды не меняется, {r} = 0, однако имеется поток вещества через поверхность разрыва 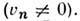Альвеновский Р. м. движется относительно этой поверхности впереди и позади неё со скоростью альвеновской волны На альвеновском разрыве полная напряжённость магн. поля 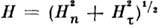непрерывна, однако сам вектор Н поворачивается вокруг нормали к поверхности разрыва на нек-рый угол. Термодинамич. параметры при переходе через альвеновский разрыв непрерывны, {s}= О, { р} = 0, а скачки тангенциальных компонент скорости и магн. поля связаны ф-лой: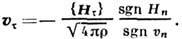

В случае анизотропного давления () на альвеновском (вращательном) разрыве плотность и внутр. энергия, а также магн. поле могут тоже испытывать скачки, к-рые связаны соотношениями:

Разрывы, движущиеся относительно среды на к-рых плотность среды испытывает скачок, наз. ударными волнами. На ударных волнах возрастает энтропия,а также практически для

всех видов веществ растут давление и плотность:

Ударные волны плоско поляризованы, т. е. векторы H₁, Н₂ и нормаль к поверхности разрыва лежат в одной плоскости. Скорость ударной волны относительно вещества перед ней зависит от её амплитуды, т. е. от величины скачка к.-л. МГД-параметра, напр. { р}. При стремлении амплитуды ударной волны к нулю её скорость стремится к скорости линейных магнитозвуковых волн, быстрой u_f или медленной u_s. Зависимость между значениями термодинамич. параметров перед волной и позади неё наз. ударной адиабатой или адиабатой Гюгоньо. Различают параллельные, перпендикулярные и косые ударные волны.

Эволюционность и устойчивость разрывов магнито-гидродинамических. Р. м., устойчивые относительно распада на неск. разрывов или нестационарных течений, наз. эволюционными. Любое бесконечно малое возмущение эволюц. разрыва приводит (по крайней мере на достаточно малых промежутках времени) к малым изменениям МГД-параметров разрыва. Возмущения эволюц. разрыва могут нарастать во времени по экспоненц. закону (как expgt с положит. инкрементом g), что свидетельствует о неустойчивости такого разрыва, однако в течение времени возмущение останется малым. Введение понятия эволюционности Р. м. связано с возможностью построения нестационарных решений с заданными нач. условиями. Если линеаризованная задача о взаимодействии малых возмущений с разрывом не имеет решения либо имеет не единств. решение, что указывает на неправомерность исходного предположения о малости амплитуд возмущений в течение малого, но конечного времени, то разрыв наз. неэволюционным. Неэволюц. разрыв в течение короткого времени (в модели идеальной магн. гидродинамики - мгновенно) распадается на неск. устойчивых разрывов или может перейти в нестационарное течение. Альвеновские, тангенциальные и контактные Р. м. относятся к классу эволюционных. Для ударных волн условие эволюционности накладывает ограничения на скорость разрыва относительно среды. В частности, скорость быстрой ударной волны относительно среды перед ней должна быть больше скорости быстрой магнитозвуковой волны в среде u_f1, а скорость относительно среды за ней - меньше скорости быстрой магнитозвуковой волны u_f2.

При падении волн на сильный разрыв коэф. отражения может превысить единицу, т. е. волна усиливается в процессе отражения.

Структура разрывов. При учёте неидеальности вещества (вязкости, теплопроводности, джоулева нагрева) поверхность сильного разрыва размывается в узкий переходный слой, в к-ром МГД-параметры изменяются быстро, но непрерывно. Характер изменения параметров среды в переходной области наз. структурой разрыва. Толщина переходной области для слабой ударной волны часто превышает длину свободного пробега частиц. Это позволяет использовать ур-ния магн. гидродинамики с учётом малых диссипативных факторов для исследования структуры разрыва, к-рая часто описывается монотонной ф-цией. В разреженной плазме парные кулоновские столкновения могут быть весьма редкими и структура разрыва будет определяться коллективными процессами, а толщина переходной зоны может быть существенно меньше длины свободного пробега (напр., бесстолкновителъные ударные волны).

Лит.: Куликовский А. Г., Любимов Г. А., Магнитная гидродинамика, М., 1962; Plasma Electrodynamics, v. 2, Oxf., 1975; Баранов В. Б., Краснобаев К. В., Гидродинамическая теория космической плазмы, М., 1977; Арци-мович Л. А., Сагдеев Р. 3., Физика плазмы для физи-

ков, М., 1979; Половин Р. В., Демуцкий В, П., Основы магнитной гидродинамики, М., 1987.

Н. С. Ерохин, О. Г. Онищенко,

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.