ПРОТЕКАНИЯ ТЕОРИЯ

ПРОТЕКАНИЯ ТЕОРИЯ

(перколяции теория, от лат. percolatio - процеживание; просачивания теория) - матем. теория, к-рая используется в физике для изучения процессов, происходящих в неоднородных средах со случайными свойствами, но зафиксированными в пространстве и неизменными во времени. Возникла в 1957 в результате работ Дж. Хаммерсли (J. Hammersley). В П. т. различают решёточные задачи П. т., континуальные задачи и т. н. задачи на случайных узлах. Решёточные задачи в свою очередь делятся на т. н. задачи узлов н задачи связей между ними.

Задачи связей. Пусть связи - рёбра, соединяющие соседние узлы бесконечной периодич. решётки (рис., о). Предполагается, что связи между узлами могут быть двух типов: целыми или разорванными (блокированными). Распределение целых и блокированных связей в решётке случайно; вероятность того, что данная связь является целой, равна х. Предполагается, что она не зависит от состояния соседних связей. Два узла решётки считаются связанными друг с другом, если их соединяет цепочка целых связей. Совокупность связанных друг с другом узлов наз. кластером. При малых значениях x целые связи, как правило, далеки друг от друга и доминируют кластеры из небольшого кол-ва узлов, однако с увеличением x размеры кластеров резко увеличиваются. Порогом протекания ( х _c )наз. такое значение х, при к-ром впервые возникает кластер из бесконечного числа узлов. П. т. позволяет вычислить пороговые значения х _с, а также исследовать топологию крупномасштабных кластеров вблизи порога (см. Фракталы). С помощью П. т. можно описать электропроводность системы, состоящей из проводящих и непроводящих элементов. Напр., если предположить, что целые связи проводят электрич. ток, а блокированные не проводят, то окажется, что при х < х _с уд. электропроводность решётки равна О, а при х > х _с она отлична от 0.

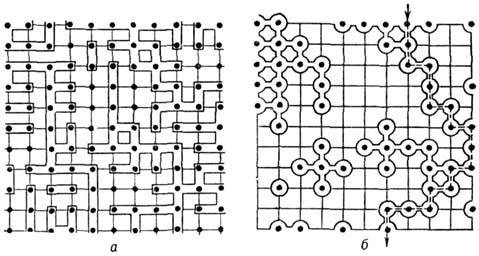
Протекание по решётке: а - задача связей (путь протекания сквозь указанный блок отсутствует); б - задача узлов (показан путь протекания).

Решёточные задачи узлов отличаются от задач связей тем, что блокированные связи распределены на решётке не поодиночке - блокируются все связи, выходящие из к.-л. узла (рис., б). Блокированные таким способом узлы распределены на решётке случайно, с вероятностью 1 - х. Доказано, что порог х _с для задачи связей на любой решётке не превышает порога х _с для задачи узлов на той же решётке. Для нек-рых плоских решёток найдены точные значения х _с. Напр., для задач связей на треугольной и шестиугольной решётках х _с= 2sin(p/18) и х _с=1 - 2sin(p/18). Для задачи узлов на квадратной решётке х _с =0,5. Для трёхмерных решёток значения х _с найдены приближённо с помощью моделирования на ЭВМ (табл.).

Пороги протекания для различных решёток

Тип решётки	х с для задачи связей	х с Для задачи узлов
Плоские решётки
шестиугольная	0,6527	0,7
квадратная	0,5	0,59
треугольная	0,3473	0,5
Трёхмерные решётки
типа алмаза	0,39	0,43
простая кубическая	0,25	0,31
объёмноцентрированная кубическая	0, 18	0,25
гранецентрированная кубическая	0,12	0,2

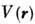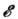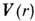Континуальные задачи. В этом случае вместо протекания по связям и узлам рассматриваются явления переноса в неупорядоченной сплошной среде. Во всём пространстве задаётся непрерывная случайная ф-ция координат . Зафиксируем нек-рое значение ф-ции и назовём области пространства, в к-рых 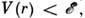чёрными. При достаточно малых значениях эти области редки и, как правило, изолированы друг от друга, а при достаточно больших они занимают почти всё пространство. Требуется найти т. н. уровень протекания 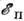- мин. значение 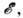при к-ром чёрные области образуют связанный лабиринт путей, уходящий на бесконечное расстояние. В трёхмерном случае точное решение континуальной задачи пока не найдено. Однако моделирование на ЭВМ показывает, что для гауссовых случайных ф-ций 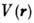в трёхмерном пространстве при доля объёма, занимаемая чёрными областями, приолижённо равно 0,16. В двумерном случае доля площади, занимаемая чёрными областями при 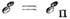, точно равна 0,5.

Задачи на случайных узлах. Пусть узлы не образуют правильную решётку, а случайно распределены в пространстве. Два узла считаются связанными, если расстояние между ними не превышает фиксированное значение 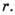Если 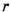мало по сравнению со ср. расстоянием между узлами, то кластеры, содержащие 2 или больше связанных друг с другом узлов, редки, однако число таких кластеров резко растёт с увеличением г и при нек-ром критич. значении 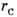возникает бесконечный кластер. Моделирование на ЭВМ показывает, что в трёхмерном случае 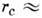0,86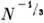, где N- концентрация узлов. Задачи на случайных узлах и их разл. обобщения играют важную роль в теории прыжковой проводимости.

Эффекты, описываемые П. т., относятся к критическим явлениям, характеризующимся критич. точкой, вблизи к-рой система распадается на блоки, причём размер отд. блоков неограниченно растёт при приближении к критич. точке. Возникновение бесконечного кластера в задачах П. т. во многом аналогично фазовому переходу второго рода. Для матем. описания этих явлений вводится параметр порядка, к-рым в случае решёточных задач служит доля Р(х )узлов решётки, принадлежащих к бесконечному кластеру. Вблизи порога протекания ф-ция Р(х )имеет вид

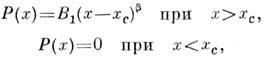
где 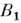- численный коэф., b - критич. индекс параметра порядка. Аналогичная ф-ла описывает поведение уд. электропроводности s(х )вблизи порога протекания: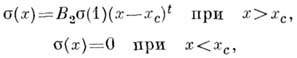

где В ₂- численный коэф., s(1) - уд. электропроводность при c= 1, f - критич. индекс электропроводности. Пространственные размеры кластеров характеризуются радиусом корреляции R(x), обращающимся в

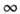
при

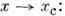
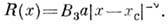
Здесь B₃ - численный коэф., а- постоянная решётки, v - критич. индекс радиуса корреляции.

Пороги протекания существенно зависят от типа задач П. т., но критич. индексы одинаковы для разл. задач и определяются лишь размерностью пространства d (универсальность). Представления, заимствованные из теории фазовых переходов 2-го рода, позволяют получить соотношения, связывающие различные критич. индексы. Приближение самосогласованного поля применимо к задачам П. т. при d >6. В этом приближении критич. индексы не зависят от d; b = 1, 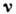=¹/₂.

Результаты П. т. используются при изучении электронных свойств неупорядоченных систем, фазовых переходов металл- диэлектрик, ферромагнетизма твёрдых растворов, кинетич. явлений в сильно неоднородных средах, физ.-хим. процессов в твёрдых телах и т. д.

Лит.: Мотт Н., Дэвис Э., Электронные процессы в некристаллических веществах, пер. с англ., 2 изд., т. 1-2, М., 1982; Шкловский Б. И., Эфрос А. Л., Электронные свойства легированных полупроводников, м., 1979; 3 а й-ман Д. М., Модели беспорядка, пер. с англ., М., 1982; Эфрос А. Л., Физика и геометрия беспорядка, М., 1982; Соколов И. М., Размерности и другие геометрические критические показатели в теории протекания, "УФН", 1986, т. 150 с. 221. А. Л. Эфрос.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.