ПОНДЕРОМОТОРНЫЕ СИЛЫ

ПОНДЕРОМОТОРНЫЕ СИЛЫ

в звуковом поле - совокупность сил, действующих на вещество или тело, помещённое в звуковом поле. В П. с. вносят вклад переменное звуковое давление, пропорциональное амплитуде звука, и квадратичные эффекты - ра-диац. давление, силы Бьеркнеса (см. ниже), а также гидродинамич. силы, обусловленные движением среды в звуковой волне. П. с. проявляются в действии звуковой волны на чувствит. элементы приёмников звука, в УЗ-коагуляции, диспергировании, кавитации, в возникновении акустических течений, усталости материалов, подвергающихся длит. воздействию интенсивного акустич. излучения, во вспучивании границ раздела двух сред.

Сила, действующая на элемент объёма и равная где - объёмная плотность П. с., определяется изменением импульса (см. Импульс звуковой волны )элемента объёма в единицу времени, равным импульсу, втекающему в объём через его поверхность. Если тензор плотности потока импульса - то i-я компонента силы, действующая на объём определяется выражением

где dS - элемент поверхности, ограничивающий объём, а - внешняя по отношению к объёму нормаль. Соответственно этому сила, действующая на элемент поверхности dS, равна потоку импульса через него и определяется выражением В частности, на поверхности единичной площади действует сила, i -я компонента к-рой Тензор плотности потока импульса звуковой волны

где p- звуковое давление, - компонента колебательной скорости частиц, - символ Кронекера (= 1 при i=k,d_ik= 0 при ik),- тензор вязких напряжений, - плотность среды. Если поверхность жёсткая, то скорость частиц среды, прилегающих к ней, обращается в нуль и сила, действующая на единицу её площади, равна Осн. вклад в силу при таких условиях даёт звуковое давление р, и именно эта величина воспринимается чувствит. элементами приёмников звука. Для монохро-матич. звуковых волн р - гармонич. ф-ция времени, меняющаяся с частотой звука. В жидкостях при интенсивности звука характерной для ряда практич. применений в УЗ-технологии, р=Па. Такие силы могут превысить порог прочности жидкости и вызвать кавитацию. Средняя по времени П. с., обусловленная звуковым давлением в гармонич. звуковых полях, равна нулю.

Помимо этого в звуковых полях возникают постоянные во времени П. с. Они определяются квадратичными членами тензора плотности потока импульса, усреднёнными по периоду колебаний звука. Отличные от нуля эти члены по порядку величины равны плотности энергии звуковой волны: Обычно эти силы можно рассматривать как результат действия радиац. давления, или давления звукового излучения. Их величина мала, напр. 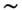в воздухе Па при интенсивности звука в воде 10 Па при интенсивности звука 1Тем не менее они приводят к заметным эффектам, проявляющимся, напр., в появлении акустич. течений, во вспучивании границ раздела двух сред и даже в возникновении фонтанчиков жидкости.

П. с. значит. величины действуют не только на элементы среды, в к-рой возбуждено звуковое поле, но и на граничащие с ней поверхности, а также на тела, находящиеся в среде. Так, напр., на взвешенное в акустич. поле тело, размеры к-рого много меньше длины звуковой волны l, а плотность равна плотности окружающей среды, в звуковом поле действует сила, заставляющая его колебаться вместе с частицами среды. При отличии плотности тела от плотности окружающей среды возникает движение тела относительно среды, причём если то оно отстаёт от частиц среды, а если - то опережает их. Движение тела относительно среды вызывает дополнит. движение среды (рассеянную волну), а значит, и дополнит. силу реакции, действующую на тело. Напр., на жёсткую сферу радиуса при в поле плоской бегущей звуковой волны действует сила

где - волновое число звуковой волны, E- средняя по времени плотность энергии акустич. поля, Если вблизи одного из тел в звуковом поле имеется другое, то влияние на первое тело рассеянной волны, исходящей от второго тела, приводит к появлению добавочной силы. Эта сила имеет характер вторичного радиац. давления и приводит к взаимодействию тел в звуковом поле. В частности, две сферы с радиусами a и b, пульсирующие в звуковом поле на расстоянии 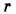друг от друга, притягиваются друг к другу с силой

где - колебат. скорости поверхностей сфер, - сдвиг фаз их колебаний,- плотности среды; наз. силой Бьеркнеса. Между осциллирующими сферами возникают более слабые силы взаимодействия; для двух сфер, осциллирующих в звуковом поле под действием звука со скоростями центральная составляющая этой силы равна

(- угол между направлением колебаний тел и линий, соединяющих их центры).

Наряду с силами акустич. происхождения, зависящими от сжимаемости среды, на тела, помещённые в звуковое поле, действуют также силы, вызванные движением тела относительно среды. Такие силы наз. гидродинамическими. К их числу относится сила сопротивления, к-рую испытывает тело, движущееся с пост. скоростью в вязкой жидкости. Для жёсткой сферы радиуса движущейся со скоростью эта сила выражается ф-лой Стокса:где - коэф. динамич. вязкости среды. Др. примером гидродинамич. силы является сила Бернулли, притягивающая тела, движущиеся в жидкости или омываемые ею. Для случая двух жёстких сфер с радиусами a и Ъ, находящихся на расстоянии друг от друга в потоке жидкости, движущейся со скоростью сила Бернулли равна

Эта сила действует, в частности, на находящиеся в звуковом поле жёсткие частицы, малые по сравнению с l. Заметим, что в случае возникновения акустич. течений и микропотоков при кавитации различие между гидродинамич. силами и усреднёнными по времени П. с. бывает чисто условным.

П. с. используется в разнообразных приёмниках звука, устройствах, измеряющих его интенсивность ( радиометр, Рэлея диск). На действии П. с. основаны эффекты коагуляции, дегазации жидкостей и металлов, диспергирования твёрдых тел в жидкости, эмульгирования и т. п., применяемые в УЗ-технологии.

Лит.: Ландау Л. Д., Лифшиц E. М., Механика сплошных сред, 2 изд., М., 1954; Бергман Л., Ультразвук и его применение в науке и технике, пер. с нем., 2 изд., М., 1957, гл. 6; Лебедев П. Н., Собр. соч., М., 1963, с. 68; Красильников В. А., Крылов В. В., Введение в физическую акустику, М., 1984. Я. А. Наугольных.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.